
【题目】如图,在边长为 4 的等边△ABC 中,点 D 从点A 开始在射线 AB 上运动,速度为 1 个单位/秒,点F 同时从 C 出发,以相同的速度沿射线 BC 方向运动,过点D 作 DE⊥AC,连结 DF 交射线 AC 于点 G

(1)当 DF⊥AB 时,求 t 的值;
(2)当点 D 在线段 AB 上运动时,是否始终有 DG=GF?若成立,请说明理由。
(3)聪明的斯扬同学通过测量发现,当点 D 在线段 AB 上时,EG 的长始终等于 AC 的一半,他想当点D 运动到图 2 的情况时,EG 的长是否发生变化?若改变,说明理由;若不变,求出 EG 的长。
【答案】(1)![]() ;(2)见详解;(3)不变.
;(2)见详解;(3)不变.
【解析】
(1)设AD=x,则BD=4-x,BF=4+x.当DF⊥AB时,通过解直角△BDF求得x的值,易得t的值;
(2)如图1,过点D作DH∥BC交AC于点H,构建全等三角形:△DHG≌△FCG,结合全等三角形的对应边相等的性质和图中相关线段间的和差关系求得DG=GF;
(3)过F作FH⊥AC,可证△ADE≌△CFH,得DE=FH,AC=EH,再证△GDE≌△GFH,可得EG=GH,即可解题.
解:(1)设AD=x,则BD=4-x,BF=4+x.
当DF⊥AB时,∵∠B=60°,
∴∠DFB=30°,
∴BF=2BD,即4+x=2(4-x),
解得x=![]() ,
,
故t=![]() ;
;
(2)如图1,过点D作DH∥BC交AC于点H,则∠DHG=∠FCG.

∵△ABC是等边三角形,
∴△ADH是等边三角形,
∴AD=DH.
又AD=CF,
∴DH=FC.
∵在△DHG与△FCG中,
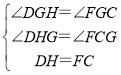 ,
,
∴△DHG≌△FCG(AAS),
∴DG=GF;
(3)如图2,过F作FH⊥AC,
在△ADE和△CFH中,
 ,
,
∴△ADE≌△CFH(AAS),
∴DE=FH,AE=CH,
∴AC=EH,
在△GDE和△GFH中,
 ∴△GDE≌△GFH(AAS),
∴△GDE≌△GFH(AAS),
∴EG=GH,
∴EG=![]() EH=
EH=![]() AC.
AC.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=21m,∠BAC=53°,求这颗古杉树AB的长度.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)当x为何值时,y>0?当x为何值时,y<0?
(3)写出y随x的增大而减小的自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验初中组织了“英语手抄报”征集活动,现从中随机抽取部分作品,按A、B、C、D四个等级进行评价,并根据统计结果绘制了如下两幅不完整的统计图.

(1)抽取了_____份作品;
(2)此次抽取的作品中等级为B的作品有______份,并补全条形统计图;
(3)若该校共征集到600份作品,请估计等级为A的作品约有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出了甲、乙两种新品饮料,它们都由A、B、C三种溶液组成,只是甲种饮料每瓶装有200克A溶液,200克B溶液,100克C溶液;乙种饮料每瓶装有100克A溶液,100克B溶液,300克C溶液,甲、乙两种饮料每瓶成本价均为瓶中A、B、C三种溶液的成本价之和.已知C种溶液每一百克的成本价为1元,乙种饮料每瓶售价为10元,利润率为![]() ,甲种饮料每瓶的利润率为20%,求这两种饮料的销售利润率为24%时,该公司销售甲、乙两种饮料的数量之比是_____.
,甲种饮料每瓶的利润率为20%,求这两种饮料的销售利润率为24%时,该公司销售甲、乙两种饮料的数量之比是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等边三角形ABC的顶点B与原点O重合,点C在x轴上,点C坐标为(6,0),等边三角形ABC的三边上有三个动点D、E、F(不考虑与A、B、C重合),点D从A向B运动,点E从B向C运动,点F从C向A运动,三点同时运动,到终点结束,且速度均为1cm/s,设运动的时间为ts,解答下列问题:
(1)求证:如图①,不论t如何变化,△DEF始终为等边三角形.
(2)如图②过点E作EQ∥AB,交AC于点Q,设△AEQ的面积为S,求S与t的函数关系式及t为何值时△AEQ的面积最大?求出这个最大值.
(3)在(2)的条件下,当△AEQ的面积最大时,平面内是否存在一点P,使A、D、Q、P构成的四边形是菱形,若存在请直接写出P坐标,若不存在请说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
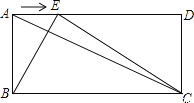
(1)若a=5,AC=13,求b.
(2)若a=5,b=10,当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com