
【题目】如图,方格纸中每个小正方形的边长均为1,点A、B、C、D均在小正方形的顶点上,
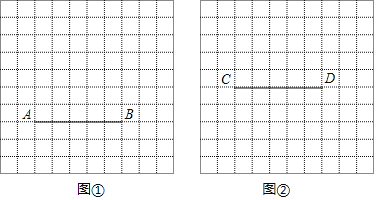
(1)在图①中画出以线段AB为一条边的菱形ABEF,点E、F在小正方形顶点上,且菱形ABEF的面积为20;
(2)在图②中画出以CD为对角线的矩形CGDH,G、H点在小正方形顶点上,点G在CD的下方,且矩形CGDH的面积为10,CG>DG.并直接写出矩形CGDH的周长.
科目:初中数学 来源: 题型:
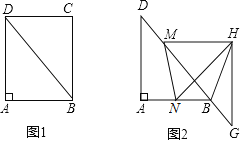
【题目】如图1在矩形ABCD中,AB=6,BC=8,△BCD沿BD的方向匀速平移得到△MGH,速度为1cm/s:同时点N从点B出发,沿BA方向匀速移动,速度为1cm/s,当点N停止移动时,△MGH也停止移动,如图2,设移动时间为t(0<t<6),连接MN,HB,HN
解答下列问题
(1)当t为何值时,MN∥HG?
(2)设四边形ADMN面积为y(cm2),求y和t之间的函数关系式;
(3)是否存在某一时刻t,使S△HBN:S四边形ADMN=2:3?若存在,求出t值:若不存在,请说明理由;
(4)是否存在某一时刻t,使MN=HB?若存在,求出t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化历史悠久,包罗万象.某校为了加强学生对中华传统文化的认识和理解,营造校园文化氛围,举办了“弘扬中华传统文化,做新时代的中学生”的知识竞赛.以下是从七年、八年两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
(1)根据上面的数据,将下列表格补充完整,整理、描述数据:
| 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
七年 | 1 | 2 | 6 | ||
八年 | 0 | 1 | 10 | 1 | 8 |
(说明:成绩90分及以上为优秀,60分以下为不合格)分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年 | 84 | 88.5 | |
八年 | 84.2 | 74 |
(2)为调动学生学习传统文化的积极性,七年级根据学生的成绩制定了奖励标准,凡达到或超过这个标准的学生将获得奖励.如果想让一半左右的学生能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”);
(3)若八年级有800名学生,试估计八年级学生成绩优秀的人数;

查看答案和解析>>
科目:初中数学 来源: 题型:
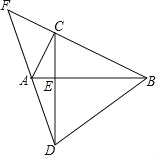
【题目】如图,Rt△ABC中,∠ACB=90°,CD⊥AB于E,CD=AB,DA、BC延长线交于F.
(1)若AC=12,∠ABC=30°,求DE的长;
(2)若BC=2AC,求证:DA=![]() FC.
FC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设慢车离乙地的距离为y1(km),快车离乙地的距离为y2(km),慢车行驶时间为x(h),两车之间的距离为S(km),y1,y2与x的函数关系图象如图①所示,S与x的函数关系图象如图②所示:
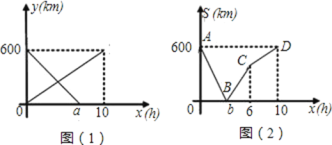
(1)图中的a=______,b=______.
(2)求快车在行驶的过程中S关于x的函数关系式.
(3)直接写出两车出发多长时间相距200km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线ABy=kx﹣1分别交x轴、y轴于点A、B,直线CDy=x+2分别交x轴、y轴于点D、C,且直线AB、CD交于点E,E的横坐标为﹣6.
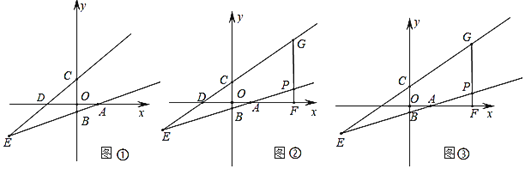
(1)如图①,求直线AB的解析式;
(2)如图②,点P为直线BA第一象限上一点,过P作y轴的平行线交直线CD于G,交x轴于F,在线段PG取点N,在线段AF上取点Q,使GN=QF,在DG上取点M,连接MN、QN,若∠GMN=∠QNF,求![]() 的值;
的值;
(3)在(2)的条件下,点E关于x轴对称点为T,连接MP、TQ,若MP∥TQ,且GN:NP=4:3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的顶点M是直线
的顶点M是直线![]() 和直线y=x+m的交点.
和直线y=x+m的交点.
(1)若直线y=x+m过点D(0,-3),求M点的坐标及二次函数![]() 的解析式;
的解析式;
(2)试证明无论m取任何值,二次函数![]() 的图象与直线y=x+m总有两个不同的交点;
的图象与直线y=x+m总有两个不同的交点;
(3)在(1)的条件下,若二次函数![]() 的图象与y轴交于点C,与x的右交点为A,试在直线
的图象与y轴交于点C,与x的右交点为A,试在直线![]() 上求异于M的点P,使P在△CMA的外接圆上.
上求异于M的点P,使P在△CMA的外接圆上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.
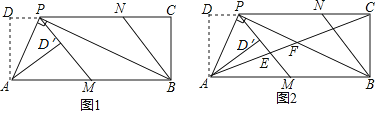
(1)求证:AD2=DPPC;
(2)请判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC,分别交PM,PB于点E,F.若![]() =
=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com