
����Ŀ���л��Ļ���ʷ�ƾã���������ijУΪ�˼�ǿѧ�����л���ͳ�Ļ�����ʶ�����⣬Ӫ��У�Ļ���Χ���ٰ��ˡ������л���ͳ�Ļ�������ʱ������ѧ������֪ʶ�����������Ǵ����ꡢ���������꼶�����ȡ20��ͬѧ�IJ��Գɼ����е���������ɼ����£�
��1��������������ݣ������б����������������������ݣ�
| 50��x��59 | 60��x��69 | 70��x��79 | 80��x��89 | 90��x��100 |
���� | 1 | 2 | 6 | ||
���� | 0 | 1 | 10 | 1 | 8 |
��˵�����ɼ�90�ּ�����Ϊ���㣬60������Ϊ���ϸ������ݣ�
�꼶 | ƽ���� | ��λ�� | ���� |
���� | 84 | 88.5 | |
���� | 84.2 | 74 |
��2��Ϊ����ѧ��ѧϰ��ͳ�Ļ��Ļ����ԣ����꼶����ѧ���ijɼ��ƶ��˽����������ﵽ���������ѧ������ý������������һ�����ҵ�ѧ���ܻ�Ӧ������ ����ȷ���������ȽϺ��ʣ����ƽ��������������������λ��������
��3�������꼶��800��ѧ�����Թ��ư��꼶ѧ���ɼ������������

���𰸡���1��3��8��89��77������2����λ������3�����ư��꼶ѧ���ɼ����������ԼΪ320�ˣ�
��������
��1�����������и��������ݣ�ֱ���ҳ��𰸼��ɣ�
��2��������λ���Ķ��弴�ɵõ����ۣ�
��3����800�����꼶ѧ���ɼ������������ռ�İٷֱȼ��ɵõ����ۣ�
�⣺��1���������⣬�ã����꼶������70��x��79����3�ˣ�
80��x��89����8�ˣ�
���꼶֪ʶ�����ijɼ�������Ϊ89��
���꼶֪ʶ�����ijɼ�����λ��Ϊ��![]() ��77��
��77��
�ཫ���б��������������Ҵ��ϵ�������Ϊ��3��8��89��77����
��2���������һ�����ҵ�ѧ���ܻ�Ӧ������λ����ȷ���������ȽϺ��ʣ�
�ʴ�Ϊ����λ����
��3��800��![]() ��320���ˣ�
��320���ˣ�
�𣺹��ư��꼶ѧ���ɼ����������ԼΪ320�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
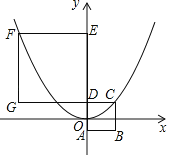
����Ŀ����ͼ���ı���ABCD��DEFG���������Σ��߳��ֱ�Ϊm��n��m��n��������ԭ��OΪAD���е㣬A��D��E��y���ϣ������κ���y��ax2��ͼ���C��F���㣬��![]() ��_____��
��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
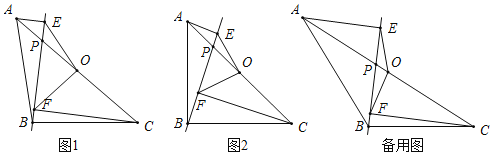
����Ŀ������ABC�У�AB=BC����O��AC���е㣬��P��AC�ϵ�һ�����㣨��P�����A��O��C�غϣ�������A����C��ֱ��BP�Ĵ��ߣ�����ֱ�Ϊ��E�͵�F������OE��OF��
��1����ͼ1����ֱ��д���߶�OE��OF��������ϵ��
��2����ͼ2������ABC=90��ʱ�����ж��߶�OE��OF֮���������ϵ��λ�ù�ϵ����˵������
��3����|CF��AE|=2��EF=2![]() ������POFΪ����������ʱ����ֱ��д���߶�OP�ij���
������POFΪ����������ʱ����ֱ��д���߶�OP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
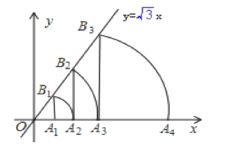
����Ŀ����ͼ,ֱ��y=![]() x,��A
x,��A![]() ����Ϊ(1,0),����A
����Ϊ(1,0),����A![]() ��x��Ĵ��߽�ֱ���ڵ�
��x��Ĵ��߽�ֱ���ڵ�![]() ,��ԭ��OΪԲ��,OB
,��ԭ��OΪԲ��,OB![]() ��Ϊ�뾶������x���ڵ�A
��Ϊ�뾶������x���ڵ�A![]() ;�ٹ���A
;�ٹ���A![]() ��x��Ĵ��߽�ֱ���ڵ�B
��x��Ĵ��߽�ֱ���ڵ�B![]() ,��ԭ��OΪԲ��,OB
,��ԭ��OΪԲ��,OB![]() ��Ϊ�뾶������x���ڵ�A
��Ϊ�뾶������x���ڵ�A![]() ,��,��������������ȥ,��A
,��,��������������ȥ,��A![]() ������Ϊ___.
������Ϊ___.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
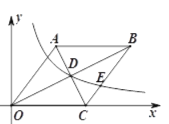
����Ŀ����ͼ������OABC�ı�OC��x���������ϣ���B������Ϊ��8��4����
��1����������εı߳���
��2��������������![]() �������ζԽ��ߵĽ���D�������BC���ڵ�E���������E�����꣮
�������ζԽ��ߵĽ���D�������BC���ڵ�E���������E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijĦ�г���2011���һ���ڶ����ȸ��²�������ͳ��ͼ�����н�����ȷ���ǣ�������
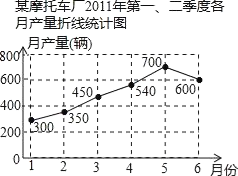
A.�ڶ������²�����350��
B.3�µ�4�µ��²����������
C.��1�µ�6���²���������
D.2�·ݱ�1�·��²���������50��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
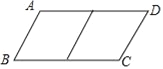
����Ŀ���ڱ߲���ȵ�ƽ���ı���ֽƬ����ȥһ�����Σ�����һ���ı��Σ���Ϊ��һ�β����������µ��ı���ֽƬ���ټ�ȥһ�����Σ���ʣ��һ���ı��Σ���Ϊ�ڶ��β��������������ƣ�����n�β��������µ��ı��������Σ����ԭƽ���ı���Ϊn�����Σ����磺��ͼ1��ABCD�У���AB=1��BC=2����ABCDΪ1�����Σ�
��1���������жϣ�
�ڱ߳��ֱ�Ϊ1��3��ƽ���ı������� �������Σ�
�ڱ߳��ֱ�Ϊ3��4��ƽ���ı������� �������Σ�
��2��������̽������㣺
����֪ABCD���ڱ߳��ֱ�Ϊ2��a��a��2��������3�����Σ��뻭��ABCD���ü��ߵ�ʾ��ͼ������ͼ���·�д��a��ֵ��
����֪ABCD���ڱ߳��ֱ�Ϊa��b��a��b��������a=7b+r��b=4r����д��ABCD�Ǽ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳���Ϊ1����A��B��C��D����С�����εĶ����ϣ�
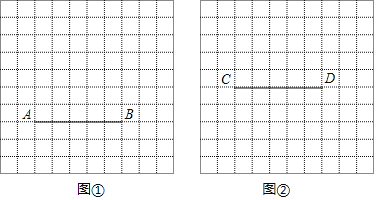
(1)��ͼ���л������߶�ABΪһ���ߵ�����ABEF����E��F��С�����ζ����ϣ�������ABEF�����Ϊ20��
(2)��ͼ���л�����CDΪ�Խ��ߵľ���CGDH��G��H����С�����ζ����ϣ���G��CD���·����Ҿ���CGDH�����Ϊ10��CG��DG����ֱ��д������CGDH���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽������֪���κ���![]() ������
������![]() .
.
��1����ú����ı���ʽ��
��2����ͼ��ʾ����![]() �����������ڵڶ������ڵ�һ�����㣬�ҵ�
�����������ڵڶ������ڵ�һ�����㣬�ҵ�![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ������
������![]() ��
��![]() ��
��![]() .
.
����![]() �����
�����![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
����![]() ����������ֵ���������ʱ��
����������ֵ���������ʱ��![]() ������.
������.
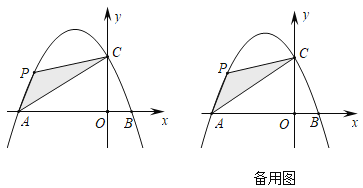
��չ����ƽ��ֱ������ϵ�У���![]() ������Ϊ
������Ϊ![]() ��
��![]() ������Ϊ
������Ϊ![]() ����������
����������![]() ���߶�
���߶�![]() ��������ͬ�Ľ��㣬��ֱ��д��
��������ͬ�Ľ��㣬��ֱ��д��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com