
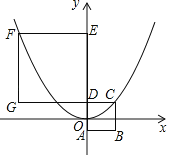
【题目】如图,四边形ABCD、DEFG都是正方形,边长分别为m、n(m<n).坐标原点O为AD的中点,A、D、E在y轴上.若二次函数y=ax2的图象过C、F两点,则![]() =_____.
=_____.
科目:初中数学 来源: 题型:
【题目】已知AM是△ABC的中线,点D在线段AM上[点D不与点A重合),过点D作DF∥AB交AC边于点F,过点C作CE∥AM交DF的延长线于点E,连接AE.
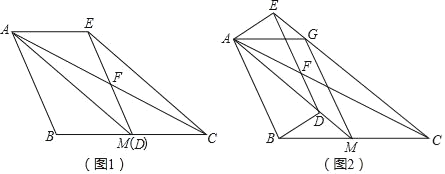
(1)如图1,当点D与点M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与点M重合时,过点M作MG∥DE交EC于点G,连接BD、AG在不添加任何辅助线的情况下,请直接写出图中所有的平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于自变量为![]() 的函数,当
的函数,当![]() 时,其函数值也为
时,其函数值也为![]() ,则称点
,则称点![]() 为此函数的不动点.若函数
为此函数的不动点.若函数![]() 图象上有两个不动点
图象上有两个不动点![]() 、
、![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求函数
,求函数![]() 的不动点坐标;
的不动点坐标;
(2)求证;![]() ;
;
(3)若函数![]() ,
,![]() ,
,![]() ,当
,当![]() 时,
时,
①求证:![]() ;
;
②求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
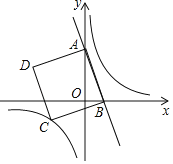
【题目】如图,直线y=﹣3x+3与y轴交于点A,与x轴交于点B,以线段AB为边,在线段AB的左侧作正方形ABCD,点C在反比例函数y=![]() (k≠0)的图象上,当正方形ABCD沿x轴正方向向右平移_____个单位长度时,正方形ABCD的一个顶点恰好落在该反比例函数图象上.
(k≠0)的图象上,当正方形ABCD沿x轴正方向向右平移_____个单位长度时,正方形ABCD的一个顶点恰好落在该反比例函数图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
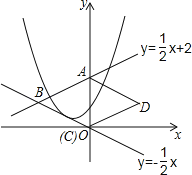
【题目】如图,直线y=![]() x+2与y轴交于点A,与直线y=﹣
x+2与y轴交于点A,与直线y=﹣![]() x交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣
x交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣![]() x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
A.﹣2![]() B.﹣2≤h≤1C.﹣1
B.﹣2≤h≤1C.﹣1![]() D.﹣1
D.﹣1![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
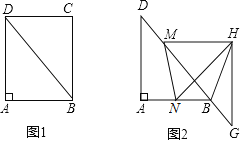
【题目】如图1在矩形ABCD中,AB=6,BC=8,△BCD沿BD的方向匀速平移得到△MGH,速度为1cm/s:同时点N从点B出发,沿BA方向匀速移动,速度为1cm/s,当点N停止移动时,△MGH也停止移动,如图2,设移动时间为t(0<t<6),连接MN,HB,HN
解答下列问题
(1)当t为何值时,MN∥HG?
(2)设四边形ADMN面积为y(cm2),求y和t之间的函数关系式;
(3)是否存在某一时刻t,使S△HBN:S四边形ADMN=2:3?若存在,求出t值:若不存在,请说明理由;
(4)是否存在某一时刻t,使MN=HB?若存在,求出t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化历史悠久,包罗万象.某校为了加强学生对中华传统文化的认识和理解,营造校园文化氛围,举办了“弘扬中华传统文化,做新时代的中学生”的知识竞赛.以下是从七年、八年两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
(1)根据上面的数据,将下列表格补充完整,整理、描述数据:
| 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
七年 | 1 | 2 | 6 | ||
八年 | 0 | 1 | 10 | 1 | 8 |
(说明:成绩90分及以上为优秀,60分以下为不合格)分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年 | 84 | 88.5 | |
八年 | 84.2 | 74 |
(2)为调动学生学习传统文化的积极性,七年级根据学生的成绩制定了奖励标准,凡达到或超过这个标准的学生将获得奖励.如果想让一半左右的学生能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”);
(3)若八年级有800名学生,试估计八年级学生成绩优秀的人数;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com