
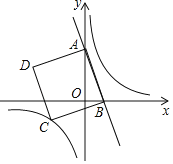
【题目】如图,直线y=﹣3x+3与y轴交于点A,与x轴交于点B,以线段AB为边,在线段AB的左侧作正方形ABCD,点C在反比例函数y=![]() (k≠0)的图象上,当正方形ABCD沿x轴正方向向右平移_____个单位长度时,正方形ABCD的一个顶点恰好落在该反比例函数图象上.
(k≠0)的图象上,当正方形ABCD沿x轴正方向向右平移_____个单位长度时,正方形ABCD的一个顶点恰好落在该反比例函数图象上.
【答案】![]() 或4
或4
【解析】
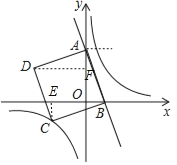
根据题意直线关系式可先求出点C的坐标,进而求出反比例函数的k值,然后分类讨论正方形的哪个点恰好落在该反比例函数图象上进而解答.
解:当x=0时,y=﹣3×0+3=3,∴A(0,3),即OA=3;
当y=0时,即0=﹣3x+3,
∴x=1,∴B(1,0),即OB=1;
过点C作CE⊥x轴,垂足为E,过点D作DF⊥y轴,垂足为F,
∵ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠CBE+∠ABO=90°
又∵CE⊥x轴
∴∠CEB=90°=∠AOB,
∴∠ECB+∠CBE=90°
∴∠ECB=∠ABO,
∴△AOB≌△BEC (AAS)
∴BE=AO=3,CE=OB=1,
同理可证△ADF≌△ABO,得DF=AO=3,AF=OB=1
∴C(﹣2,﹣1)D(﹣3,2)
将C(﹣2,﹣1)代入y=![]() 得:k=2
得:k=2
∴y=![]() ;
;
(1)当y=3时,即3=![]() ,∴x=
,∴x=![]() , 即当正方形ABCD沿x轴正方向向右平移
, 即当正方形ABCD沿x轴正方向向右平移![]() 个单位,点A落在反比例函数的图象上;
个单位,点A落在反比例函数的图象上;
(2)当y=2时,即2=![]() ,∴x=1,D沿着x轴向右平移1+3=4个单位落在反比例的图象上,即当正方形ABCD沿x轴正方向向右平移4个单位,点D落在反比例函数的图象上;
,∴x=1,D沿着x轴向右平移1+3=4个单位落在反比例的图象上,即当正方形ABCD沿x轴正方向向右平移4个单位,点D落在反比例函数的图象上;
故答案为:![]() 或4
或4


科目:初中数学 来源: 题型:
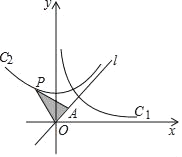
【题目】如图,曲线C2是双曲线C1:y=![]() (x>0)绕原点O逆时针旋转60°得到的图形,P是曲线C2上任意一点,点A在直线l:y=
(x>0)绕原点O逆时针旋转60°得到的图形,P是曲线C2上任意一点,点A在直线l:y=![]() x上,且PA=PO,则△POA的面积等于( )
x上,且PA=PO,则△POA的面积等于( )
A.![]() B.6C.3D.12
B.6C.3D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;(2)求点B到直线OM的距离.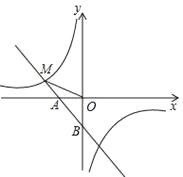
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝,![]() 是自然数)的函数解析式;
是自然数)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①这100个日需求量所组成的一组数据的中位数和众数分别是________,________;
②以100天记录的各需求量的频率作为计算平均一天需求量对应的权重.若花店计划一天购进16枝或17枝玫瑰花,从盈利的角度分析,你认为应购进16枝还是17枝?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
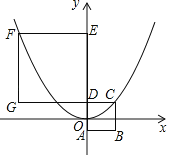
【题目】如图,四边形ABCD、DEFG都是正方形,边长分别为m、n(m<n).坐标原点O为AD的中点,A、D、E在y轴上.若二次函数y=ax2的图象过C、F两点,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
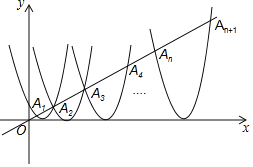
【题目】如图所示,在平面直角坐标系xOy中,抛物线![]() 与直线y=
与直线y=![]() 相交于点A1,A2,将抛物线y1向右平移后得抛物线y2,y2与直线y=
相交于点A1,A2,将抛物线y1向右平移后得抛物线y2,y2与直线y=![]() x交于点A2,A3,再将抛物线y2继续向右平移得抛物线y3,y3与直线y=
x交于点A2,A3,再将抛物线y2继续向右平移得抛物线y3,y3与直线y=![]() x交于点A3,A4……依此类推,请回答以下问题:
x交于点A3,A4……依此类推,请回答以下问题:
(1)求点A1,点A2的坐标.
(2)求抛物线y2的解析式.
(3)求AnAn+1的长(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为抛物线的顶点为D,求出点C,D的坐标,并判断△BCD的形状;
(3)点P是直线BC上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为![]() 个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.
个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某摩托车厂2011年第一、第二季度各月产量折线统计图,下列结论正确的是( )
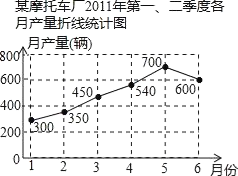
A.第二季度月产量共350辆
B.3月到4月的月产量增长最快
C.从1月到6月月产量逐渐增长
D.2月份比1月份月产量增加了50辆
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com