
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝,![]() 是自然数)的函数解析式;
是自然数)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①这100个日需求量所组成的一组数据的中位数和众数分别是________,________;
②以100天记录的各需求量的频率作为计算平均一天需求量对应的权重.若花店计划一天购进16枝或17枝玫瑰花,从盈利的角度分析,你认为应购进16枝还是17枝?请说明理由.
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 与x轴、分别交于点A、B两点(点A在点B的左边),与y轴交于点C.连接CA、CB.
与x轴、分别交于点A、B两点(点A在点B的左边),与y轴交于点C.连接CA、CB.
(1)直接写出抛物线的顶点坐标 ;∠BCO= °;
(2)点P是抛物线对称轴上一个动点, 当PA+PC的值最小时,点P的坐标是 ;
(3)在(2)的条件下,以点O为圆心,OA长为半径画⊙O,点F为⊙O上的动点,![]() 值最小,则最小值是 ;
值最小,则最小值是 ;
(4)点D是直线BC上方抛物线上的一点,是否存在点D使∠BCD=∠CAO-∠ACO,若存在,求出点D的坐标,若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
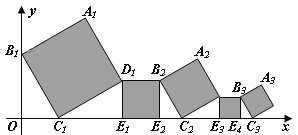
【题目】如图,在平面直角坐标系中放置5个正方形,点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O﹦60,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
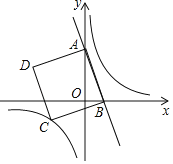
【题目】如图,直线y=﹣3x+3与y轴交于点A,与x轴交于点B,以线段AB为边,在线段AB的左侧作正方形ABCD,点C在反比例函数y=![]() (k≠0)的图象上,当正方形ABCD沿x轴正方向向右平移_____个单位长度时,正方形ABCD的一个顶点恰好落在该反比例函数图象上.
(k≠0)的图象上,当正方形ABCD沿x轴正方向向右平移_____个单位长度时,正方形ABCD的一个顶点恰好落在该反比例函数图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
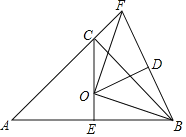
【题目】如图,AB为等腰直角△ABC的斜边(AB为定长线段),E为AB的中点,F为AC延长线上的一个动点,线段FB的垂直平分线交线段CE于点O,D为垂足,当F点运动时,给出下列四个结论,其中一定正确的结论有_____(请填写正确序号)
①O为△ABF的外心;②OF⊥OB;③![]() CE+FC=AB;④FCOB=OEFB
CE+FC=AB;④FCOB=OEFB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com