
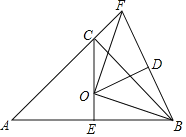
【题目】如图,AB为等腰直角△ABC的斜边(AB为定长线段),E为AB的中点,F为AC延长线上的一个动点,线段FB的垂直平分线交线段CE于点O,D为垂足,当F点运动时,给出下列四个结论,其中一定正确的结论有_____(请填写正确序号)
①O为△ABF的外心;②OF⊥OB;③![]() CE+FC=AB;④FCOB=OEFB
CE+FC=AB;④FCOB=OEFB
【答案】①②④
【解析】
①只要证明OA=OB=OF即可.②利用“8字型”证明∠FCJ=∠JOB=90°即可.③先证明![]() EC+CF=AF,再判断.④正确.证明△OEB∽△FCB即可.
EC+CF=AF,再判断.④正确.证明△OEB∽△FCB即可.
如图,连接AO.

∵CA=CB,AE=EB,
∴CE⊥AB,
∴OA=OB,
∵OD垂直平分线段BF,
∴OF=OB,
∴OA=OF=OB,
∴点O是△ABF的外心,故①正确,
设BC交OF于J.
∵AC=BC,CO=CO,AO=BO,
∴△ACO≌△BCO(SSS),
∴∠CAO=∠CBO,
∵OA=OF,
∴∠CAO=∠CFJ,
∴∠CFJ=∠OBJ,
∵∠CJF=∠OJB,
∴∠JOB=∠JCF=90°,
∴OF⊥OB,故②正确,
∵![]() CE=AC,AC+CF=AF,
CE=AC,AC+CF=AF,
显然AF不一定等于AB,故③错误.
∵∠EBC=∠OBF=45°,
∴∠EBO=∠CBF,
∵∠OEB=∠FCB=90°,
∴△OEB∽△FCB,
∴![]() ∴FCOB=OEFB,故④正确,
∴FCOB=OEFB,故④正确,
故答案为:①②④.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】2018年国务院机构改革不再保留国家卫生和计划生育委员会,组建国家卫生健康委员会,在修正人口普查数据中的低龄人口漏登后,我们估计了1982-2030年育龄妇女情况.1982年中国15-49岁育龄妇女规模为2.5亿,到2011年达3.8亿人的峰值,2017年降至3.5亿,预计到2030年将降至3.0亿.则数据2.5亿、3.8亿、3.5亿、3.0亿的中位数、平均数、方差分别是( )
A.3.25亿、3.2亿、0.245B.3.65亿、3.2亿、0.98
C.3.25亿、3.2亿、0.98D.3.65亿、3亿、0.245
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝,![]() 是自然数)的函数解析式;
是自然数)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①这100个日需求量所组成的一组数据的中位数和众数分别是________,________;
②以100天记录的各需求量的频率作为计算平均一天需求量对应的权重.若花店计划一天购进16枝或17枝玫瑰花,从盈利的角度分析,你认为应购进16枝还是17枝?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
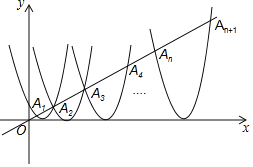
【题目】如图所示,在平面直角坐标系xOy中,抛物线![]() 与直线y=
与直线y=![]() 相交于点A1,A2,将抛物线y1向右平移后得抛物线y2,y2与直线y=
相交于点A1,A2,将抛物线y1向右平移后得抛物线y2,y2与直线y=![]() x交于点A2,A3,再将抛物线y2继续向右平移得抛物线y3,y3与直线y=
x交于点A2,A3,再将抛物线y2继续向右平移得抛物线y3,y3与直线y=![]() x交于点A3,A4……依此类推,请回答以下问题:
x交于点A3,A4……依此类推,请回答以下问题:
(1)求点A1,点A2的坐标.
(2)求抛物线y2的解析式.
(3)求AnAn+1的长(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园要修建一个截面抛物线形的拱门,其最大高度为4.5m,宽度OP为6米,现以地面(OP所在的直线)为x轴建立平面直角坐标系(如图1所示)
(1)求这条抛物线的函数表达式;
(2)如图所示,公园想在抛物线拱门距地面3米处钉两个钉子以便拉一条横幅,请计算该横幅的宽度为多少米?
(3)为修建该拱门,施工队需搭建一个矩形“支架“ABCD(由四根木杆AB﹣BC﹣CD﹣DA组成),使B,C两点在抛物线上.A,D两点在地面OP上(如图2所示),请你帮施工队计算一下最多需要准备多少米该种木杆?
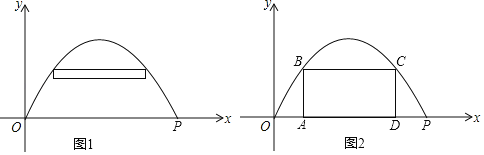
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为抛物线的顶点为D,求出点C,D的坐标,并判断△BCD的形状;
(3)点P是直线BC上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为![]() 个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.
个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化城市环境,某街道重修了路面,准备将老旧的路灯换成LED太阳能路灯,计划购买海螺臂和A字臂两种型号的太阳能路灯共100只,经过市场调查:购买海螺臂太阳能路灯1只,A字臂太阳能路灯2只共需2300元;购买海螺臂太阳能路灯3只,A字臂太阳能路灯4只共需5400元.

(1)求海螺臂太阳能路灯和A字臂太阳能路灯的单价:
(2)在实际购买时,恰逢商家活动,购买海螺臂太阳能路灯超过20只时,超过的部分打九折优惠,A字臂太阳能路灯全部打八折优惠;若规定购买的海螺臂太阳能路灯的数量不少于A字臂太阳能路灯的数量的一半,请你设计一种购买方案,使得总费用最少,并求出最小总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
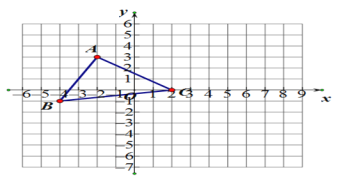
【题目】在平面直角坐标系中,△ABC的顶点坐标是A(﹣2,3),B(﹣4,﹣1), C(2,0).点P(m,n)为△ABC内一点,平移△ABC得到△A1B1C1 ,使点P(m,n)移到P(m+6,n+1)处.
(1)画出△A1B1C1
(2)将△ABC绕坐标点C逆时针旋转90°得到△A2B2C,画出△A2B2C;
(3)在(2)的条件下求BC扫过的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com