
����Ŀ����ͼ�����κ���![]() ��x�ᡢ�ֱ��ڵ�A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C������CA��CB��
��x�ᡢ�ֱ��ڵ�A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C������CA��CB��
��1��ֱ��д�������ߵĶ������� ����BCO= ��;
��2����P�������߶Գ�����һ�����㣬 ��PA+PC��ֵ��Сʱ����P�������� ��
��3���ڣ�2���������£��Ե�OΪԲ�ģ�OA��Ϊ�뾶����O����FΪ��O�ϵĶ��㣬![]() ֵ��С������Сֵ�� ��
ֵ��С������Сֵ�� ��
��4����D��ֱ��BC�Ϸ��������ϵ�һ�㣬�Ƿ���ڵ�Dʹ��BCD=��CAO����ACO�������ڣ������D�����꣬�������ڣ�˵�����ɣ�

���𰸡���1����1,4����45������2����1,2������3��![]() ����4��D������Ϊ��
����4��D��������![]() ��
��
��������
��1�����������ߵĶ��㹫ʽ����������C,B���ɣ�
��2����C����l�ĶԳƵ�,����A���C�ĶԳƵ㣬��l�ĵ㼴ΪP,��ʱPA+PC��ֵ��С.
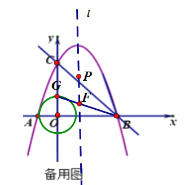
��3��ԲO��y��Ľ���ΪG������BG��BG��l�Ľ��㼴Ҫ���F�㣬��Ϊ������ģ��.
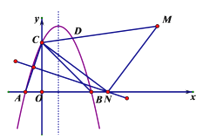
��4����AC�Ĵ�ֱƽ���ߣ���x���ڵ�N������CN����CN��NM����ȡNM=NC.����CM.��M������.���ֱ��CM�Ľ���ʽ������DΪֱ��CM�������ߵĽ��㣬�õ�D������.
��1����1,4����45��
�߶��κ���![]()
��y=-��x-1��2+4
�������ߵĶ������꣨1,4��
��C(O,3),B(3,0��
��CO=BO
���BCO=45��
��2����1,2��
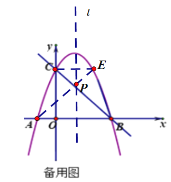
��C����l�ĶԳƵ�E,����AE����l�ĵ㼴ΪP,��ʱPA+PC��ֵ��С
��A,E����l�Գƣ�C(O,3)
��E(2,3)
��AEΪy=x+1
�ߵ�P�������߶Գ�����
��P(1,2)
��3��ԲO��y��Ľ���ΪG������BG��BG��l�Ľ��㼴Ҫ���F�㣬��Ϊ������ģ��.���![]() ��СֵΪ
��СֵΪ![]() .
.
��4����AC�Ĵ�ֱƽ���ߣ���x���ڵ�N����N������Ϊ��4��0��������CN����CN��NM����ȡNM=NC.����CM.���M������Ϊ��7,4��.ֱ��CM�Ľ���ʽΪ![]() ��
��![]() ���õ�D������Ϊ��
���õ�D������Ϊ��![]() ��.
��.
�������֪A(-1,0����C(0,3��
��AC�Ĵ�ֱƽ���ߣ���x���ڵ�N
��ô�ֱƽ����Ϊy= -![]() x+
x+ ![]()
��N��������4��0��
����CN����CN��NM����ȡNM=NC������CM
CN=MN=5��CN��NM
��M��������7,4��
�ɵ�ֱ��CM�Ľ���ʽΪ![]()
�߸���DΪֱ��CM�������ߵĽ���
��![]()
��D��������![]() ��
��
/p>



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
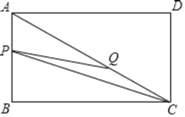
����Ŀ����ͼ���ھ���ABCD�У�AB��3��BC��4����P�ӵ�A��������A��B��C�˶����ٶ�Ϊÿ��1����λ���ȣ���Q�ӵ�C��������C��A��D�˶�����C��A�˶�ʱ���ٶ�Ϊÿ��1����λ���ȣ���A��D�˶�ʱ���ٶ�Ϊÿ��3����λ���ȣ�P��Q����ͬʱ����������Q�����Dʱ��P��Q����ͬʱֹͣ�˶�������PQ��CP������APQ�����ΪS����P���˶�ʱ��Ϊt���룩��
��1����t��6ʱ����AQ�ij���
��2������Q��C��A�˶�ʱ���ú�t�Ĵ���ʽ��ʾ��Q��AB��BC�ľ��룮
��3����S��t�ĺ�����ϵʽ��
��4���ڵ�P�˶��Ĺ����У�ֱ��д����APQ����CPQͬʱΪ�۽�������ʱt��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
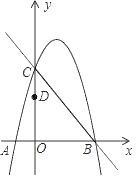
����Ŀ����ͼ��ֱ��y����x+5��x�ύ�ڵ�B����y�ύ�ڵ�C��������y����x2+bx+c��ֱ��y����x+5����B��C���㣬��֪��D������Ϊ��0��3��
��1���������ߵĽ���ʽ��
��2����M��N�ֱ���ֱ��BC��x���ϵĶ��㣬����DMN���ܳ���Сʱ�����M��N�����꣬��д����DMN�ܳ�����Сֵ��
��3����P����������һ���㣬�ڣ�2���������£��Ƿ���������ĵ�P��ʹ��PBA����ODN�������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y1��![]() x2+bx+c����ԭ�㣬��x������һ��A��4��0��������ΪP��
x2+bx+c����ԭ�㣬��x������һ��A��4��0��������ΪP��
��1����������y1�Ľ���ʽ�͵�P�����ꣻ
��2����ͼ2����Q��0��a��Ϊy����������һ�㣬����Q��x���ƽ���߽�������y1��![]() x2+bx+c�ڵ�M��N����������y1��
x2+bx+c�ڵ�M��N����������y1��![]() x2+bx+c��ֱ��MN���۵õ��µ�������y2����P���ڵ�B�������ı���BMPN���������
x2+bx+c��ֱ��MN���۵õ��µ�������y2����P���ڵ�B�������ı���BMPN���������![]() ����a��ֵ����B�����ꣻ
����a��ֵ����B�����ꣻ
��3����ͼ3���ڣ�2���������£��ڵ�һ����������y1��![]() x2+bx+c��ȡһ��C������OC����CD��OB��D��BE��OC��x����E������DE������BEO����DEA�����C�����꣮
x2+bx+c��ȡһ��C������OC����CD��OB��D��BE��OC��x����E������DE������BEO����DEA�����C�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�ǵ��������Σ�������BAC=![]() ��
��![]() <600��,D��BC���ϵ�һ�㣬����AD���߶�AD�Ƶ�A˳ʱ����ת
<600��,D��BC���ϵ�һ�㣬����AD���߶�AD�Ƶ�A˳ʱ����ת![]() ��AE������E��BC��ƽ���ߣ���AB�ڵ�F������DE��BE��DF
��AE������E��BC��ƽ���ߣ���AB�ڵ�F������DE��BE��DF
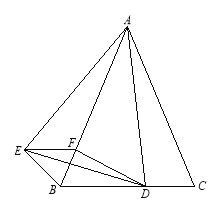
��1����֤��BE=CD
��2����AD��BC�����ж��ı���BDFE����״��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
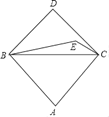
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����BCΪб��������ֱ��������BCD��E�ǡ�BCD��һ�㣬����BE��EC��BE��AB����BEC+![]() ��BAC��180�㣮��EC��1��tan��ABC��
��BAC��180�㣮��EC��1��tan��ABC��![]() �����߶�BD�ij���_____��
�����߶�BD�ij���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������C2��˫����C1��y��![]() ��x��0����ԭ��O��ʱ����ת60��õ���ͼ�Σ�P������C2������һ�㣬��A��ֱ��l��y��
��x��0����ԭ��O��ʱ����ת60��õ���ͼ�Σ�P������C2������һ�㣬��A��ֱ��l��y��![]() x�ϣ���PA��PO�����POA��������ڣ�������
x�ϣ���PA��PO�����POA��������ڣ�������
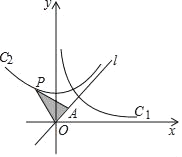
A.![]() B.6C.3D.12
B.6C.3D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018�����Ժ�����ĸﲻ�ٱ������������ͼƻ�����ίԱ�ᣬ�齨������������ίԱ�ᣬ�������˿��ղ������еĵ����˿�©�Ǻ����ǹ�����1982-2030�����举Ů���.1982���й�15-49�����举Ů��ģΪ2.5�ڣ���2011���3.8���˵ķ�ֵ��2017�꽵��3.5�ڣ�Ԥ�Ƶ�2030�꽫����3.0��.������2.5�ڡ�3.8�ڡ�3.5�ڡ�3.0�ڵ���λ����ƽ����������ֱ���( )
A.3.25�ڡ�3.2�ڡ�0.245B.3.65�ڡ�3.2�ڡ�0.98
C.3.25�ڡ�3.2�ڡ�0.98D.3.65�ڡ�3�ڡ�0.245
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ÿ����ÿ֦5Ԫ�ļ۸��ũ����������֦õ�廨��Ȼ����ÿ֦10Ԫ�ļ۸����.������������꣬ʣ�µ�õ�廨����������.
��1��������һ�칺��16֦õ�廨�����������![]() ����λ��Ԫ�����ڵ���������
����λ��Ԫ�����ڵ���������![]() ����λ��֦��
����λ��֦��![]() ����Ȼ�����ĺ�������ʽ��
����Ȼ�����ĺ�������ʽ��
��2�������¼��100��õ�廨��������������λ��֦�����������±���
�������� | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Ƶ�� | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
����100��������������ɵ�һ�����ݵ���λ���������ֱ���________��________��
����100���¼�ĸ���������Ƶ����Ϊ����ƽ��һ����������Ӧ��Ȩ��.������ƻ�һ�칺��16֦��17֦õ�廨����ӯ���ĽǶȷ���������ΪӦ����16֦����17֦����˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com