
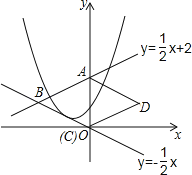
【题目】如图,直线y=![]() x+2与y轴交于点A,与直线y=﹣
x+2与y轴交于点A,与直线y=﹣![]() x交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣
x交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣![]() x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
A.﹣2![]() B.﹣2≤h≤1C.﹣1
B.﹣2≤h≤1C.﹣1![]() D.﹣1
D.﹣1![]()
【答案】A
【解析】
将y=![]() x+2与y=-
x+2与y=-![]() x联立可求得点B的坐标,然后由抛物线的顶点在直线y=-
x联立可求得点B的坐标,然后由抛物线的顶点在直线y=-![]() x可求得k=-
x可求得k=-![]() h,于是可得到抛物线的解析式为y=(x-h)2-
h,于是可得到抛物线的解析式为y=(x-h)2-![]() h,由图形可知当抛物线经过点B和点C时抛物线与菱形的边AB、BC均有交点,然后将点C和点B的坐标代入抛物线的解析式可求得h的值,从而可判断出h的取值范围.
h,由图形可知当抛物线经过点B和点C时抛物线与菱形的边AB、BC均有交点,然后将点C和点B的坐标代入抛物线的解析式可求得h的值,从而可判断出h的取值范围.
解:∵将y=![]() x+2与y=﹣
x+2与y=﹣![]() x联立得:
x联立得: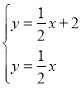 ,解得:
,解得:![]() .
.
∴点B的坐标为(﹣2,1).
由抛物线的解析式可知抛物线的顶点坐标为(h,k).
∵将x=h,y=k,代入得y=﹣![]() x得:﹣
x得:﹣![]() h=k,解得k=﹣
h=k,解得k=﹣![]() h,
h,
∴抛物线的解析式为y=(x﹣h)2﹣![]() h.
h.
如图1所示:当抛物线经过点C时.
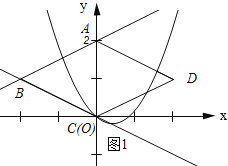
将C(0,0)代入y=(x﹣h)2﹣![]() h得:h2﹣
h得:h2﹣![]() h=0,解得:h1=0(舍去),h2=
h=0,解得:h1=0(舍去),h2=![]() .
.
如图2所示:当抛物线经过点B时.
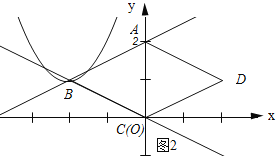
将B(﹣2,1)代入y=(x﹣h)2﹣![]() h得:(﹣2﹣h)2﹣
h得:(﹣2﹣h)2﹣![]() h=1,整理得:2h2+7h+6=0,解得:h1=﹣2,h2=﹣
h=1,整理得:2h2+7h+6=0,解得:h1=﹣2,h2=﹣![]() (舍去).
(舍去).
综上所述,h的范围是﹣2≤h≤![]() .
.
故选:A.


科目:初中数学 来源: 题型:
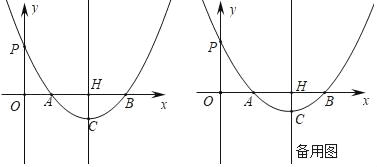
【题目】如图,在平面直角坐标系中,二次函数y=a(x﹣1)(x﹣5)(a>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于P点,过其顶点C作直线CH⊥x轴于点H.
(1)若∠APB=30°,请直接写出满足条件的点P的坐标;
(2)当∠APB最大时,请求出a的值;
(3)点P、O、C、B能否在同一个圆上?若能,请求出a的值,若不能,请说明理由.
(4)若a=![]() ,在对称轴HC上是否存在一点Q,使∠AQP=∠ABP?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
,在对称轴HC上是否存在一点Q,使∠AQP=∠ABP?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)在(1)的条件下,设20名学生测试成绩的众数是a,中位数是b,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
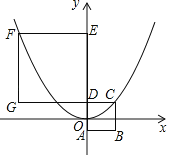
【题目】如图,四边形ABCD、DEFG都是正方形,边长分别为m、n(m<n).坐标原点O为AD的中点,A、D、E在y轴上.若二次函数y=ax2的图象过C、F两点,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
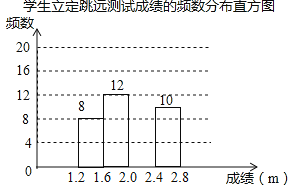
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
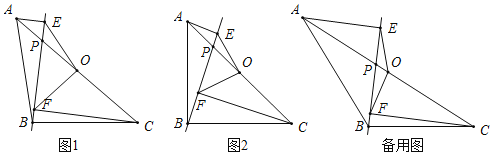
【题目】在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由
(3)若|CF﹣AE|=2,EF=2![]() ,当△POF为等腰三角形时,请直接写出线段OP的长.
,当△POF为等腰三角形时,请直接写出线段OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
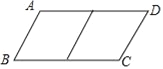
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作后,余下的四边形是菱形,则称原平行四边形为n阶准菱形,例如:如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
(1)理解与判断:
邻边长分别为1和3的平行四边形是 阶准菱形;
邻边长分别为3和4的平行四边形是 阶准菱形;
(2)操作、探究与计算:
①已知ABCD的邻边长分别为2,a(a>2),且是3阶准菱形,请画出ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知ABCD的邻边长分别为a,b(a>b),满足a=7b+r,b=4r,请写出ABCD是几阶准菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com