
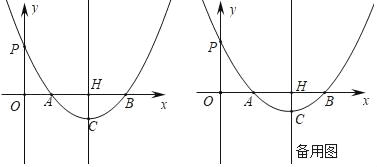
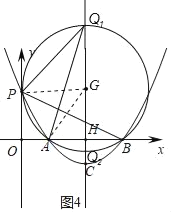
【题目】如图,在平面直角坐标系中,二次函数y=a(x﹣1)(x﹣5)(a>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于P点,过其顶点C作直线CH⊥x轴于点H.
(1)若∠APB=30°,请直接写出满足条件的点P的坐标;
(2)当∠APB最大时,请求出a的值;
(3)点P、O、C、B能否在同一个圆上?若能,请求出a的值,若不能,请说明理由.
(4)若a=![]() ,在对称轴HC上是否存在一点Q,使∠AQP=∠ABP?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
,在对称轴HC上是否存在一点Q,使∠AQP=∠ABP?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)点P坐标为(0,![]() )或(0,
)或(0,![]() );(2)
);(2)![]() ;(3)能,a的值为
;(3)能,a的值为![]() ;(4)点Q坐标为(3,3+
;(4)点Q坐标为(3,3+![]() )或(3,3﹣
)或(3,3﹣![]() ).
).
【解析】
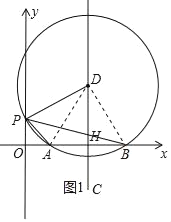
(1)作△PAB的外接圆⊙D,连接DP、DA、DB,证△ABD是等边三角形,求A(1,0),B(5,0),得DP=DA=AB=4,H(3,0),得直线CH:x=3,求出D(3,2![]() )
)
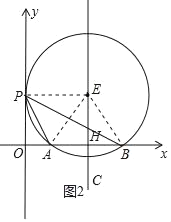
设P(0,p)(p>0),由PD2=32+(2![]() ﹣p)2=42,求出P的坐标;(2)作△PAB的外接圆⊙E,连接EP、EA、EB,如图2,由切线性质,得四边形OHEP是矩形,在Rt△AEH中,EH=
﹣p)2=42,求出P的坐标;(2)作△PAB的外接圆⊙E,连接EP、EA、EB,如图2,由切线性质,得四边形OHEP是矩形,在Rt△AEH中,EH=![]() ,求出0P得点P坐标为(0,
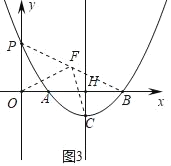
,求出0P得点P坐标为(0,![]() ),代入抛物线解析式可得;(3)连接PB,取PB中点F,连接FO、FC,证点P、O、B在以点F为圆心、FB的长为半径的圆上,若点C在⊙F上,则FC=FB,由抛物线解析式y=a(x﹣1)(x﹣5)=ax2﹣6ax+5a=a(x﹣3)2﹣4a,得P(0,5a),C(3,﹣4a),再求F坐标,由
),代入抛物线解析式可得;(3)连接PB,取PB中点F,连接FO、FC,证点P、O、B在以点F为圆心、FB的长为半径的圆上,若点C在⊙F上,则FC=FB,由抛物线解析式y=a(x﹣1)(x﹣5)=ax2﹣6ax+5a=a(x﹣3)2﹣4a,得P(0,5a),C(3,﹣4a),再求F坐标,由![]() ,得
,得![]() ,解方程可得;(4)作△PAB的外接圆⊙G,连接GP、GA,设⊙G与直线CH交于点Q,得∠AQP=∠ABP,当a=
,解方程可得;(4)作△PAB的外接圆⊙G,连接GP、GA,设⊙G与直线CH交于点Q,得∠AQP=∠ABP,当a=![]() 时,点P(0,1),设G(3,b)(b>0),由GP=GA,得32+(b﹣1)2=(3﹣1)2+b2,进一步得G(3,3),GQ=GA=
时,点P(0,1),设G(3,b)(b>0),由GP=GA,得32+(b﹣1)2=(3﹣1)2+b2,进一步得G(3,3),GQ=GA=![]() ,可得点Q坐标有两种可能.
,可得点Q坐标有两种可能.
解:(1)作△PAB的外接圆⊙D,连接DP、DA、DB,如图1
∴DP=DA=DB,
∵C为抛物线顶点且CH⊥x轴
∴CH为抛物线对称轴,即CH垂直平分AB
∴D在直线CH上
∵∠APB=30°
∴∠ADB=2APB=60°
∴△ABD是等边三角形
∵当y=0时,a(x﹣1)(x﹣5)=0 解得:x1=1,x2=5
∴A(1,0),B(5,0)
∴DP=DA=AB=4,H(3,0),直线CH:x=3
∴AH=2,DH=![]() AH=2
AH=2![]()
∴D(3,2![]() )
)
设P(0,p)(p>0)
∴PD2=32+(2![]() ﹣p)2=42
﹣p)2=42
解得:p1=![]() ,p2=
,p2=![]()
∴点P坐标为(0,![]() )或(0,
)或(0,![]() )
)
(2)作△PAB的外接圆⊙E,连接EP、EA、EB,如图2
∵∠AEB=2∠APB
∴∠AEB最大时,∠APB最大
∵AB=4是定值
∴EH最小时,∠AEB最大,此时⊙E与y轴相切于点P
∴EP⊥y轴于P
∴四边形OHEP是矩形
∴PE=OH=3
∴EA=PE=3
∴Rt△AEH中,EH=![]()
∴OP=EH=![]()
∴点P坐标为(0,![]() ),代入抛物线解析式得:5a=
),代入抛物线解析式得:5a=![]()
∴a=![]()
(3)点P、O、C、B能在同一个圆上.
连接PB,取PB中点F,连接FO、FC
∵∠POB=90°
∴OF=PF=FB=![]() PB
PB
∴点P、O、B在以点F为圆心、FB的长为半径的圆上
若点C在⊙F上,则FC=FB
∵抛物线解析式y=a(x﹣1)(x﹣5)=ax2﹣6ax+5a=a(x﹣3)2﹣4a
∴P(0,5a),C(3,﹣4a)
∵B(5,0),F为PB中点
∴F![]()
∴![]()
∴![]()
解得:a1=![]() ,a2=﹣
,a2=﹣![]() (舍去)
(舍去)
∴a的值为![]()
(4)对称轴HC上存在一点Q,使∠AQP=∠ABP
作△PAB的外接圆⊙G,连接GP、GA,设⊙G与直线CH交于点Q
∴∠AQP=∠ABP
当a=![]() 时,点P(0,1)
时,点P(0,1)
设G(3,b)(b>0)
∴GP2=32+(b﹣1)2,GA2=(3﹣1)2+b2
∵GP=GA
∴32+(b﹣1)2=(3﹣1)2+b2
解得:b=3
∴G(3,3),GQ=GA=![]()
∴点Q坐标为(3,3+ ![]() )或(3,3﹣
)或(3,3﹣![]() ).
).


科目:初中数学 来源: 题型:
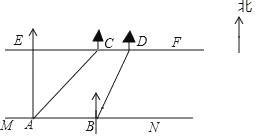
【题目】在社会实践课上,小聪所在小组要测量一条小河的宽度,如图,河岸EF∥MN,小聪在河岸MN上的点A处测得河对岸小树C位于东北方向,然后向东沿河岸走了30米,到达B处测得河对岸小树D位于北偏东30°的方向,又有同学测得CD=10米
(1)∠EAC= 度,∠DBN= 度;
(2)求小河的宽度AE.(结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
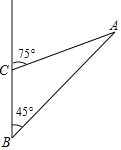
【题目】成都市第十三次党代会提出实施“东进”战略,推动了城市发展格局“千年之变”成都龙泉山城市森林公园借“东进”之风,聚全市之力,着力打造一个令世界向往的城市中心,如图为成都市龙泉山城市豪林公园三个景点A,B,C的平面示意图,景点C在B的正北方向5千米处,景点A在B的东北方向,在C的北偏东75°方向上.
(1)∠BAC的大小
(2)求景点A,C的距离(![]() =1.414,
=1.414,![]() =1.732,sin75°≈0.966,cos75°≈0.259,tan75°≈3.732,结果精确到0.1)
=1.732,sin75°≈0.966,cos75°≈0.259,tan75°≈3.732,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM是△ABC的中线,点D在线段AM上[点D不与点A重合),过点D作DF∥AB交AC边于点F,过点C作CE∥AM交DF的延长线于点E,连接AE.
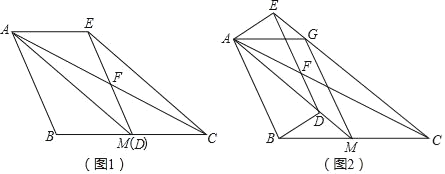
(1)如图1,当点D与点M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与点M重合时,过点M作MG∥DE交EC于点G,连接BD、AG在不添加任何辅助线的情况下,请直接写出图中所有的平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
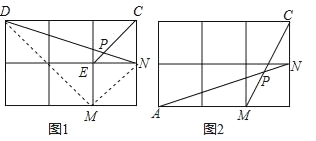
【题目】(问题呈现)如图1,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求tan∠CPN的值.
(方法归纳)求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
(问题解决)(1)直接写出图1中tan∠CPN的值为 ;
(2)如图2,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2 400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价为多少元?
(2)如果该商品的进价为25元,那么该商店3月份销售这种商品的利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
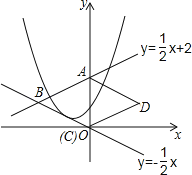
【题目】如图,直线y=![]() x+2与y轴交于点A,与直线y=﹣
x+2与y轴交于点A,与直线y=﹣![]() x交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣
x交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣![]() x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
A.﹣2![]() B.﹣2≤h≤1C.﹣1
B.﹣2≤h≤1C.﹣1![]() D.﹣1
D.﹣1![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com