
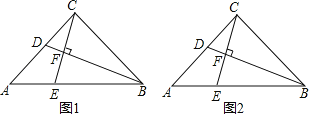
【题目】如图1,△ABC为等腰直角三角形,∠ACB=90°,AC=BC,点D和E分别是AC、AB上的点,CE⊥BD,垂足为F
(1)![]()
①求证:D为AC的中点;②计算![]() 的值.
的值.
(2)若![]() ,如图2,则
,如图2,则![]() = (直接写出结果,用k的代数式表示)
= (直接写出结果,用k的代数式表示)
【答案】(1)①见解析;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①先证明△CDF∽△BDC,再利用相似的性质即可解答
②过点A作直线BD的垂线,交BD延长线于G,则AG∥CF,得到![]() ,再利用勾股定理求出CF,BD,即可解答
,再利用勾股定理求出CF,BD,即可解答
(2)根据题意可知△CDF∽△BDC,再利用相似的性质求出![]() =k﹣1,过点A作直线BD的垂线,交BD延长线于G,则AG∥CF,得到AG=(k﹣1)CF,GD=(k﹣1)FD,再根据勾股定理即可解答
=k﹣1,过点A作直线BD的垂线,交BD延长线于G,则AG∥CF,得到AG=(k﹣1)CF,GD=(k﹣1)FD,再根据勾股定理即可解答
(1)①证明:∵∠ACB=90°,CE⊥BD,
∴∠BCD=∠CFD=90°.
∴∠BCF=∠CDF(同角的余角相等).
∴△CDF∽△BDC.
∴![]() .
.
∵![]() ,AC=BC,
,AC=BC,
∴![]() .
.
∴D为AC的中点;
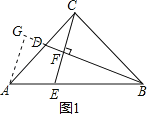
②如图1,过点A作直线BD的垂线,交BD延长线于G,则AG∥CF,
∴△ADG∽△CDF.
∴![]() .
.
∴AG=CF,GD=FD.
在直角△CFD中,CF=2DF,CD2=DF2+CF2,易得CF=![]() CD.
CD.
在直角△BCD中,BC=2CD,BD2=CD2+BC2,易得BD=![]() CD.
CD.
由tan∠EBF=tan∠ABG知,![]() .
.
∴![]() .
.
(2)∵∠ACB=90°,CE⊥BD,
∴∠BCD=∠CFD=90°.
∴∠BCF=∠CDF(同角的余角相等).
∴△CDF∽△BDC.
∴![]() .
.
∵![]() ,AC=BC,
,AC=BC,
∴![]() .
.
∴![]() =k﹣1;
=k﹣1;
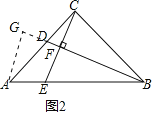
如图2,过点A作直线BD的垂线,交BD延长线于G,则AG∥CF,
∴△ADG∽△CDF.
∴![]() =k﹣1.
=k﹣1.
∴AG=(k﹣1)CF,GD=(k﹣1)FD.
在直角△CFD中,CF=kDF,CD2=DF2+CF2,易得CF=![]() .
.
在直角△BCD中,BC=kCD,BD2=CD2+BC2,易得BD=![]() CD.
CD.
由tan∠EBF=tan∠ABG知,![]() .即
.即![]()
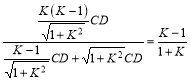 .
.
∴![]() .
.
故答案是:![]() .
.


科目:初中数学 来源: 题型:
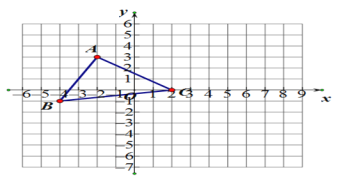
【题目】在平面直角坐标系中,△ABC的顶点坐标是A(﹣2,3),B(﹣4,﹣1), C(2,0).点P(m,n)为△ABC内一点,平移△ABC得到△A1B1C1 ,使点P(m,n)移到P(m+6,n+1)处.
(1)画出△A1B1C1
(2)将△ABC绕坐标点C逆时针旋转90°得到△A2B2C,画出△A2B2C;
(3)在(2)的条件下求BC扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的方程(a+1)x2+(2a﹣3)x+a﹣2=0有两个不相等的实根,且关于x的方程![]() 的解为整数,则满足条件的所有整数a的和是_____.
的解为整数,则满足条件的所有整数a的和是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在平面直角坐标系中.抛物线y=![]() x2+bx+c与x轴交于A两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣2).已知点E(m,0)是线段AB上的动点(点E不与点A,B重合).过点E作PE⊥x轴交抛物线于点P.交BC于点F.
x2+bx+c与x轴交于A两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣2).已知点E(m,0)是线段AB上的动点(点E不与点A,B重合).过点E作PE⊥x轴交抛物线于点P.交BC于点F.
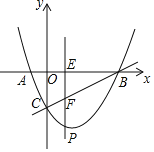
(1)求该抛物线的表达式;
(2)当线段EF,PF的长度比为1:2时,请求出m的值;
(3)是否存在这样的m,使得△BEP与△ABC相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
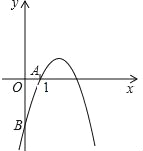
【题目】如图,抛物线y=﹣x2+5x+n经过点A(1,0),与y轴交于点B.
(1)求抛物线的解析式;
(2)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
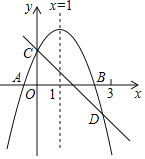
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,则下列结论:
①abc>0
②a﹣b+c<0;
③2a+b+c>0;
④x(ax+b)≤a+b;
其中正确的有_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,过二次函数
为坐标原点,过二次函数![]() 图象上的点
图象上的点![]() ,作
,作![]() 轴的垂线交
轴的垂线交![]() 轴于点
轴于点![]() .
.
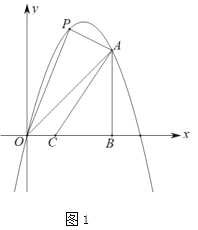
(1)如图1,![]() 为线段
为线段![]() 上方抛物线上的一点,在
上方抛物线上的一点,在![]() 轴上取点
轴上取点![]() ,点
,点![]() 、
、![]() 为
为![]() 轴上的两个动点,点
轴上的两个动点,点![]() 在点
在点![]() 的上方且
的上方且![]() 连接
连接![]() ,当四边形
,当四边形![]() 的面积最大时,求
的面积最大时,求![]() 的最小值.
的最小值.
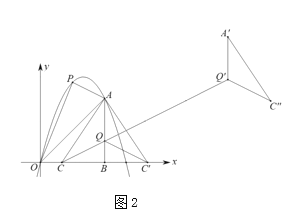
(2)如图2,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,
翻折,![]() 点的对应点为
点的对应点为![]() ,将
,将![]() 沿射线
沿射线![]() 平移
平移![]() 个单位得
个单位得![]() ,在抛物线上取一点
,在抛物线上取一点![]() ,使得以
,使得以![]() 为顶点的三角形是等腰三角形,求
为顶点的三角形是等腰三角形,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015随州)甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )

A. 4B. 3C. 2D. 1
【答案】B
【解析】
试题此题主要考查了一次函数的应用,读函数的图象的关键是理解横、纵坐标表示的意义,根据题意并结合横纵坐标的意义得出辆摩托车的速度,然后再分别分析,即可得出答案.
解:由图象可得:出发1小时,甲、乙在途中相遇,故①正确;
甲骑摩托车的速度为:120÷3=40(千米/小时),设乙开汽车的速度为a千米/小时,
则![]() ,
,
解得:a=80,
∴乙开汽车的速度为80千米/小时,
∴甲的速度是乙速度的一半,故④正确;
∴出发1.5小时,乙比甲多行驶了:1.5×(80﹣40)=60(千米),故②正确;
乙到达终点所用的时间为1.5小时,甲得到终点所用的时间为3小时,故③错误;
∴正确的有①②④,共3个,
故选:B.
考点:一次函数的应用.
【题型】单选题
【结束】
9
【题目】计算:![]() ______.
______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com