
【题目】如图,二次函数y=﹣x2+3x+m的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
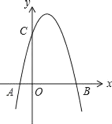
(1)求m的值及C点坐标;
(2)在抛物线的对称轴上是否存在一点M,使得它到B、C两点的距离和最小,若存在,求出此时M点坐标,若不存在,请说明理由;
(3)P为抛物线上一点,它关于直线BC的对称点为Q,当四边形PBQC为菱形时,请直接写出点P的坐标.
【答案】(1)m=4,C(0,4);(2)存在M(![]() ),见解析;(3)P(
),见解析;(3)P(![]() )或P(
)或P(![]() ).
).
【解析】
(1)用待定系数法求出抛物线解析式;
(2)先求得点C的坐标,然后依据待定系数法求得直线BC的解析式,然后再求得抛物线的对称轴方程,由三角形的三边关系可知当点P、C、B在一条直线上时,PC+PB有最小值,最后将点P的横坐标代入直线BC的解析式可求得点P的纵坐标;
(3)先判断出四边形PBQC时菱形时,点P是线段BC的垂直平分线,利用该特殊性建立方程求解.
解:(1)将B(4,0)代入y=﹣x2+3x+m,
解得,m=4,
二次函数解析式为y=﹣x2+3x+4,
令x=0,得y=4,
∴C(0,4);
(2)存在,如图所示
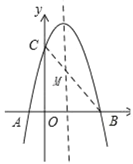
∵MC+MB≥BC,
∴当点M、C、B在一条直线上时,MC+MB有最小值.
∵点C的坐标为(0,4).
设直线BC的解析式为y=kx+4.
∵将点B、C的坐标代入得:![]() ,解得k=﹣1,b=4,
,解得k=﹣1,b=4,
∴直线BC的解析式为y=﹣x+4,
∵抛物线的对称轴为![]() ,
,
∴点M的横坐标为![]() ,
,
∵将![]() 代入直线BC的解析式得
代入直线BC的解析式得![]() ,
,
∴点M的坐标为![]() ;
;
(3)如图,
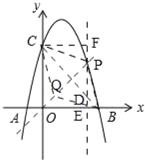
∵点P在抛物线上,
∴设P(m,﹣m2+3m+4),
当四边形PBQC是菱形时,点P在线段BC的垂直平分线上,
∵B(4,0),C(0,4)
∴线段BC的垂直平分线的解析式为y=x,
∴m=﹣m2+3m+4,
∴![]() ,
,
∴![]() 或
或![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
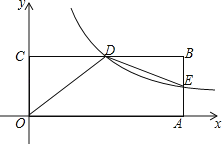
【题目】如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=![]() .
.
(1)求过点D的反比例函数的解析式;
(2)求△DBE的面积;
(3)x轴上是否存在点P使△OPD为直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线C1:y=x+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3.0),与y轴交于C(0,-3)
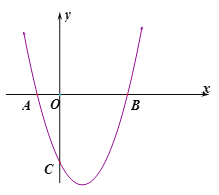
(1)求抛物线C1的表达式;
(2)分别写出抛物线C1关于B点,关于A点的对称抛物线C2, C3的函数表达式
(3)设C1的顶点为D,C2与x轴的另一个交点为A1顶点为D1,C3与x轴的另一个交点为B1,顶点为D2,在以A、B、D、A1、B1、D1、D2这七个点中的四个点为顶点的四边形中,求面积最大的四边形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮分别从甲地和乙地同时出发,沿同一条路相向而行,小明开始跑步,中途改为步行,到达乙地恰好用![]() 小亮骑自行车以
小亮骑自行车以![]() 的速度直接到甲地,两人离甲地的路程
的速度直接到甲地,两人离甲地的路程![]() 与各自离开出发地的时间
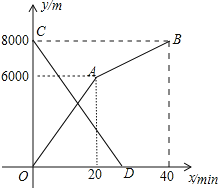
与各自离开出发地的时间![]() 之间的函数图象如图所示,
之间的函数图象如图所示,
![]() 甲、乙两地之间的路程为______m,小明步行的速度为______
甲、乙两地之间的路程为______m,小明步行的速度为______![]() ;
;
![]() 求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
![]() 求两人相遇的时间.
求两人相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现实社会中,塑料袋仍然是白色污染的一部分,为了解塑料袋的使用情况,某校八年级环保小组随机抽取“幸福小区”40户居民家庭,记录了这些家庭某个月丢弃塑料袋的数量(单位:个)如下:
29 39 35 39 39 27 33 35 31 31
32 32 34 31 33 39 38 40 38 42
31 31 38 31 39 27 33 35 40 38
29 39 35 33 39 39 38 42 37 32
请根据上述数据,解答以下问题:
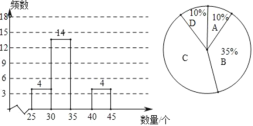
(1)若数据为x,按“组距为5”列出了如下的频数分布表,请将表中空缺的部分补充完整,并补全频数分布直方图;
分组 | 频数 |
A:25≤x<30 | 4 |
B:30≤x<35 | 14 |
C:35≤x<40 | |
D:40≤x<45 | 4 |
合计 | 40 |
(2)根据(1)中的直方图可以看出,这40户居民家庭这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
(3)根据频数分布表,画出了如图所示的扇形统计图,请求出C组对应的扇形圆心角的度数;
(4)若该小区共有1000户居民家庭,请你估计每月丢弃的塑料袋数量不小于30个的家庭户数.
查看答案和解析>>
科目:初中数学 来源: 题型:
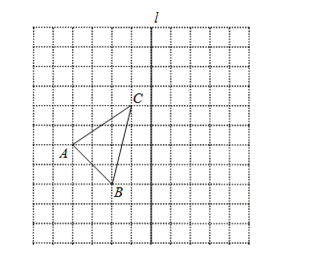
【题目】如图,在![]() 的正方形网格中,每个小正方形的边长都为1,网格中有一个格点
的正方形网格中,每个小正方形的边长都为1,网格中有一个格点![]() (即三角形的顶点都在格点上).
(即三角形的顶点都在格点上).
(1)在图中作出![]() 关于直线l对称的
关于直线l对称的![]() ;(要求A与
;(要求A与![]() ,B与
,B与![]() ,C与
,C与![]() 相对应)
相对应)
(2)作出![]() 绕点C顺时针方向旋转90°后得到的
绕点C顺时针方向旋转90°后得到的![]() ;
;
(3)在(2)的条件下求出线段CB在旋转中所扫过的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
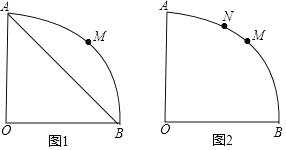
【题目】图1、图2均为圆心角为90°的扇形、请按要求用无刻度的直尺完成下列作图.
(1)在图1中、点M是![]() 的中点、请作出线段AB的垂直平分线;
的中点、请作出线段AB的垂直平分线;
(2)在图2中、点M是![]() 的中点,点N又是
的中点,点N又是![]() 的三等分点,请作出线段0B的垂直平分线.
的三等分点,请作出线段0B的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,
求两次摸 出都是红球的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com