
【题目】如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围. 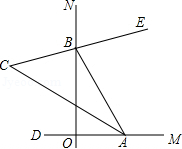
【答案】解:∠ACB的大小保持不变.理由: ∵∠ABn=90°+∠OAB,AC平分∠OAB,BE平分∠ABN,
∴∠ABE= ![]() ∠ABN=
∠ABN= ![]() (90°+∠OAB)=45°+
(90°+∠OAB)=45°+ ![]() ∠OAB,
∠OAB,
即∠ABE=45°+∠CAB,
又∵∠ABE=∠ACB+∠CAB,
∴∠ACB=45°,
故∠ACB的大小不发生变化,且始终保持45°
【解析】根据角平分线的定义、三角形的内角和、外角性质求解.
【考点精析】本题主要考查了三角形的内角和外角和三角形的外角的相关知识点,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
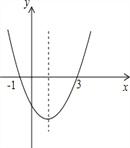
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列6个结论正确的有________个.
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b;⑤3a+c=0;⑥b+2c<0;⑦当x>1时,y随着x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( ) 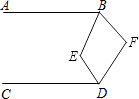
A.∠E=∠F
B.∠E+∠F=180°
C.3∠E+∠F=360°
D.2∠E﹣∠F=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别是边AB、AC的中点,将△ADE沿着DE对折,点A落在BC边上的点F,若∠B=50°,则∠BDF的度数为( ) 
A.50°
B.70°
C.75°
D.80°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com