
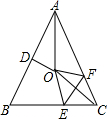
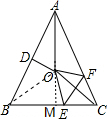
 如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是( )
如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是( )| A、45° | B、50° |
| C、55° | D、60° |


科目:初中数学 来源: 题型:
| A、0.71×10-8 |
| B、7.1×10-6 |
| C、7.1×10-7 |
| D、7.1×10-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式 |
| B、旅客上飞机前的安检,采用抽样调查方式 |
| C、了解北京市居民日平均用水量,采用全面调查方式 |
| D、了解北京市每天的流动人口数,采用抽样调查方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:
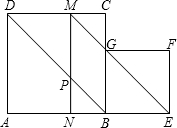 如图,在线段AE的同侧作正方形ABCD和正方形BEFG(BE<AB),连接EG并延长交DC于点M,作MN⊥AB,垂足为N,MN交BD于点P,设正方形ABCD的边长为1.
如图,在线段AE的同侧作正方形ABCD和正方形BEFG(BE<AB),连接EG并延长交DC于点M,作MN⊥AB,垂足为N,MN交BD于点P,设正方形ABCD的边长为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com