
【题目】如图,已知△ABC中AB=AC.
(1)作图:在AC上有一点D,延长BD,并在BD的延长线上取点E,使AE=AB,连AE,作∠EAC的平分线AF,AF交DE于点F(用尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,连接CF,求证:∠BAC=∠BFC.

科目:初中数学 来源: 题型:
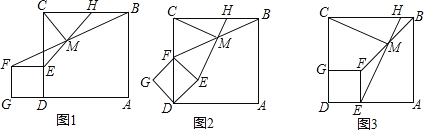
【题目】如图1,点E是正方形ABCD边CD上任意一点,以DE为边作正方形DEFG,连接BF,点M是线段BF中点,射线EM与BC交于点H,连接CM.
(1)请直接写出CM和EM的数量关系和位置关系;
(2)把图1中的正方形DEFG绕点D顺时针旋转45°,此时点F恰好落在线段CD上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由;
(3)把图1中的正方形DEFG绕点D顺时针旋转90°,此时点E、G恰好分别落在线段AD、CD上,如图3,其他条件不变,(1)中的结论是否成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
若![]() ,
,![]() ,
,![]() 为数轴上三点且点
为数轴上三点且点![]() 在
在![]() ,
,![]() 之间,若点
之间,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 的距离的3倍,我们就称点
的距离的3倍,我们就称点![]() 是
是![]() 的好点.
的好点.
如图1,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为2.表示1的点
表示的数为2.表示1的点![]() 到
到![]() 的距离是3,到
的距离是3,到![]() 的距离是1,那么点
的距离是1,那么点![]() 是
是![]() 的好点;又如,表示
的好点;又如,表示![]() 的点
的点![]() 到
到![]() 的距离是1,到
的距离是1,到![]() 的距离是3,那么点
的距离是3,那么点![]() 就不是
就不是![]() 的好点,但点
的好点,但点![]() 是
是![]() 的好点.
的好点.
知识运用:
(1)若![]() 、
、![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为2.
所表示的数为2.
数 所表示的点是![]() 的好点;
的好点;
数 所表示的点是![]() 的好点;
的好点;
(2)若点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 在点
在点![]() 的右边,且点
的右边,且点![]() 在
在![]() ,
,![]() 之间,点
之间,点![]() 是
是![]() 的好点,求点
的好点,求点![]() 所表示的数(用含
所表示的数(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(3)若![]() 、
、![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为27,现有一只电子蚂蚁
所表示的数为27,现有一只电子蚂蚁![]() 从点
从点![]() 出发,以每秒6个单位的速度向右运动,运动时间为
出发,以每秒6个单位的速度向右运动,运动时间为![]() 秒.如果
秒.如果![]() ,
,![]() ,
,![]() 中恰有一个点为其余两点的好点,求
中恰有一个点为其余两点的好点,求![]() 的值.
的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小亮、小刚、小颖一起研究一道数学题,如图,已知EF⊥AB,CD⊥AB,小明说:“如果还知道∠CDG=∠BFE,则能得到 ∠AGD=∠ACB.”
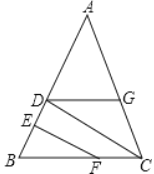
小亮说:“把小明的已知和结论倒过来,即由 ∠AGD=∠ACB ,
可得到 ∠CDG=∠BFE .”
小刚说:“∠AGD 一定大于∠BFE .”
小颖说:“如果连接 GF,则GF一定平行于AB .”
他们四人中,有____个人的说法是正确的.
查看答案和解析>>
科目:初中数学 来源: 题型:
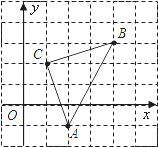
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)写出点A、B的坐标;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,写出A′B′C′的三个顶点坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级组织学生参加夏令营活动,本次夏令营分为甲、乙、丙三组进行活动.下面两幅统计图反映了学生报名参加夏令营的情况,请你根据图中的信息回答下列问题:
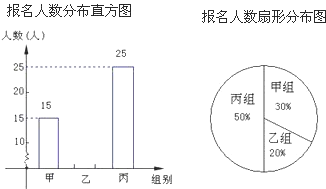
(1)该年级报名参加丙组的人数为 ;
(2)该年级报名参加本次活动的总人数 ,并补全频数分布直方图;
(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).当t为__________ 时,以B,P,Q三点为顶点的三角形是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
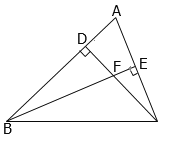
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,AC的垂直平分线BE与CD交于点F,与AC交于点E.
(1)判断△DBC的形状并证明你的结论.
(2)求证:BF=AC.
(3)试说明CE=![]() BF.
BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
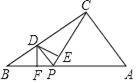
【题目】如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点P在边AB上,∠CPB的平分线交边BC于点D,DE⊥CP于点E,DF⊥AB于点F.当△PED与△BFD的面积相等时,BP的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com