
【题目】小明、小亮、小刚、小颖一起研究一道数学题,如图,已知EF⊥AB,CD⊥AB,小明说:“如果还知道∠CDG=∠BFE,则能得到 ∠AGD=∠ACB.”
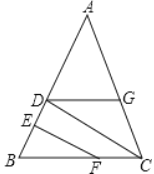
小亮说:“把小明的已知和结论倒过来,即由 ∠AGD=∠ACB ,
可得到 ∠CDG=∠BFE .”
小刚说:“∠AGD 一定大于∠BFE .”
小颖说:“如果连接 GF,则GF一定平行于AB .”
他们四人中,有____个人的说法是正确的.
科目:初中数学 来源: 题型:
【题目】 完成下面的证明.
如图,已知AB∥CD∥EF, 写出∠A,∠C,∠AFC的关系并说明理由.
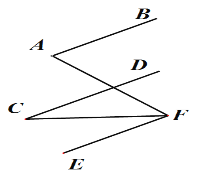
解:∠AFC= . 理由如下:
∵AB∥EF(已知),
∴∠A= (两直线平行,内错角相等).
∵CD∥EF(已知),
∴∠C= ( ).
∵∠AFC= - ,
∴∠AFC= (等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学现有在校学生2150人,为了解该校学生的课余活动情况,采取随机抽样的方法从阅读、运动、娱乐、其它四个方面调查了若干名学生,并将调查的结果绘制了如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
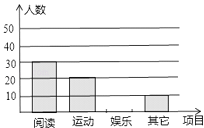
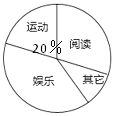
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形图,并求出扇形统计图中阅读部分圆心角的度数;
(3)请你估计该中学在课余时间参加阅读和其它活动的学生一共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年高峡水库蓄水达到了177米的设计目标水位.据测算,蓄水达到177米目标水位后,高峡水库电站的年发电量将达到842.4亿千瓦时,比2017年要多发电20%.据资料显示,火力发电时每燃烧12吨标准原煤可发电2.5万千瓦时.(千瓦时为一种能量单位)
(1)求2017年高峡电站的年发电量;
(2)请计算高峡电站2020年全年发电量与2017年全年发电量相比,可为国家多节约标准原煤多少万吨?
(3)已知2019年全年发电量比2018年增加了10%,2018年与2019年的发电量之和比2017年发电量的2倍还多129亿千瓦时,求2018年和2019年高峡电站年发电量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理a2+b2=c2本身就是一个关于a,b,c的方程,满足这个方程的正整数解(a,b,c)通常叫做勾股数组.毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:(3,4,5),(5,12,13),(7,24,25),….分析上面勾股数组可以发现,4=1×(3+1),12=2×(5+1),24=3×(7+1),…分析上面规律,第5个勾股数组为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E,若BD=6,则CE的值为( )
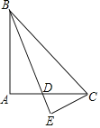
A. 4B. 3.5C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中AB=AC.
(1)作图:在AC上有一点D,延长BD,并在BD的延长线上取点E,使AE=AB,连AE,作∠EAC的平分线AF,AF交DE于点F(用尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,连接CF,求证:∠BAC=∠BFC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a,b,c表示交叉的三条公路,现要建一货物中转站,要求它到这三条公路的距离相等,则可供选择的站址最多有![]()
![]()
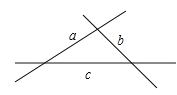
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
如图1,△ABC中,∠ACB=90°,点D在AB上,且∠BAC=2∠DCB,求证:AC=AD.
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法1:如图2,作AE平分∠CAB,与CD相交于点E.
方法2:如图3,作∠DCF=∠DCB,与AB相交于点F.
(1)根据阅读材料,任选一种方法,证明AC=AD.
用学过的知识或参考小明的方法,解决下面的问题:
(2)如图4,△ABC中,点D在AB上,点E在BC上,且∠BDE=2∠ABC,点F在BD上,且∠AFE=∠BAC,延长DC、FE,相交于点G,且∠DGF=∠BDE.
①在图中找出与∠DEF相等的角,并加以证明;
②若AB=kDF,猜想线段DE与DB的数量关系,并证明你的猜想.
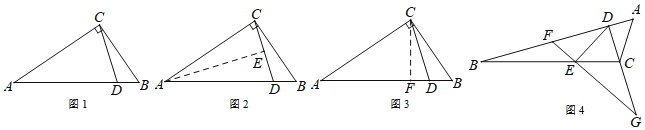
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com