
【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E,若BD=6,则CE的值为( )
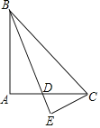
A. 4B. 3.5C. 2D. 3
【答案】D
【解析】
延长BA、CE相交于点F,利用“角边角”证明△BCE和△BFE全等,根据全等三角形对应边相等可得CE=EF,根据等角的余角相等求出∠ABD=∠ACF,然后利用“角边角”证明△ABD和△ACF全等,根据全等三角形对应边相等可得BD=CF,然后求解即可.
解:如图,
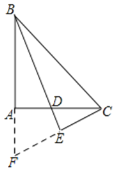
延长BA、CE相交于点F,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△BCE和△BFE中,

∴△BCE≌△BFE(ASA),
∴CE=EF,
∵∠BAC=90°,CE⊥BD,
∴∠ACF+∠F=90°,∠ABD+∠F=90°,
∴∠ABD=∠ACF,
在△ABD和△ACF中,
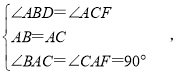
∴△ABD≌△ACF(ASA),
∴BD=CF,
∵CF=CE+EF=2CE,
∴BD=2CE=6,
∴CE=3.
故选D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】共享经济与我们的生活息息相关,其中,共享单车的使用给我们的生活带来了很多便利.但在使用过程中出现一些不文明现象.某市记者为了解“使用共享单车时的不文明行为”.随机抽查了该市部分市民,并对调查结果进行了整理,绘制了如下两幅尚不完整的统计图表(每个市民仅持有一种观点).
调查结果分组统计表
组别 | 观点 | 频数(人数) |
| 损坏零件 | 50 |
| 破译密码 | 20 |
| 乱停乱放 |
|
| 私锁共享单车,归为己用 |
|
| 其他 | 30 |
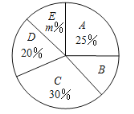
请根据以上信息,解答下列问题:
(1)填空:![]() ;
;![]() ;
;![]() ;
;
(2)求扇形图中![]() 组所在扇形的圆心角度数;
组所在扇形的圆心角度数;
(3)若该市约有100万人,请你估计其中持有![]() 组观点的市民人数.
组观点的市民人数.
(4)针对以上现象,作为初中生的你有什么合理化的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小亮、小刚、小颖一起研究一道数学题,如图,已知EF⊥AB,CD⊥AB,小明说:“如果还知道∠CDG=∠BFE,则能得到 ∠AGD=∠ACB.”
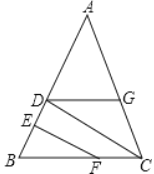
小亮说:“把小明的已知和结论倒过来,即由 ∠AGD=∠ACB ,
可得到 ∠CDG=∠BFE .”
小刚说:“∠AGD 一定大于∠BFE .”
小颖说:“如果连接 GF,则GF一定平行于AB .”
他们四人中,有____个人的说法是正确的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.



(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级组织学生参加夏令营活动,本次夏令营分为甲、乙、丙三组进行活动.下面两幅统计图反映了学生报名参加夏令营的情况,请你根据图中的信息回答下列问题:
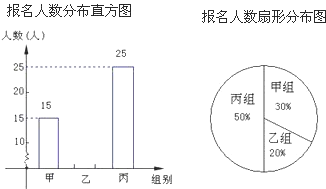
(1)该年级报名参加丙组的人数为 ;
(2)该年级报名参加本次活动的总人数 ,并补全频数分布直方图;
(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
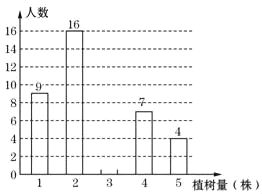
【题目】为了发展乡村旅游,建设美丽从化,某中学七年级一班同学都积极参加了植树活动,今年四月份该班同学的植树情况部分如图所示,且植树2株的人数占32%.
(1)求该班的总人数、植树株数的众数,并把条形统计图补充完整;
(2)若将该班同学的植树人数所占比例绘制成扇形统计图时,求“植树3株”对应扇形的圆心角的度数;
(3)求从该班参加植树的学生中任意抽取一名,其植树株数超过该班植树株数的平均数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
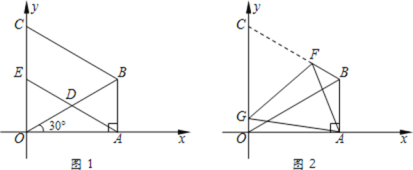
【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com