练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】先化简，再求值.

    ⑴(x＋2)2－(x＋1)(x－1), 再选取一个你喜欢的数代入x求值.

    ⑵,其中.

    【答案】（1）原式= 4x+5, 当x=0时，原式=5；

    （2）原式==-x+y,当x=-2,y=时，原式=2+=

    【解析】

    (1)原式利用完全平方公式，平方差公式计算，去括号合并得到最简结果，把x=0代入计算即可求出值．

    (2)先利用完全平方公式和平方差公式计算，再去括号、合并同类项即可化简原式，继而将x、y的值代入计算．

    解：（1）原式=x2+4x+4-x2+1=4x+5,

    当x=0时，原式=5；

    （2）原式=（x2+4xy+4y2-3x2-2xy+y2-5y2）÷(2x)=(-2x2+2xy) ÷(2x)=-x+y,

    当x=-2,y=时，原式=2+=

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

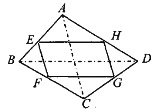
    【题目】如图，四边形 ABCD 中，E、F、G、H 分别为各边的中点，顺次连 结 E、F、G、H，把四边形 EFGH 称为中点四边形．连结 AC、BD，容易证明：中点 四边形 EFGH 一定是平行四边形．

    (1)如果改变原四边形 ABCD 的形状，那么中点四边形的形状也随之改变，通过探索 可以发现：当四边形 AB CD 的对角线满足 AC＝BD 时，四边形 EFGH 为菱形；当四边形ABCD 的对角线满足 时，四边形 EFGH 为矩形；当四边形 ABCD 的对角线满足 时，四边形 EFGH 为正方形．

    (2)试证明：S△AEH＋S△CFG＝ S□ ABCD

    (3)利用(2)的结论计算：如果四边形 ABCD 的面积为 2012， 那么中点四边形 EFGH 的面积是 （直接将结果填在 横线上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB＝AC，BE⊥AC于点E，CF⊥AB于点F，BE，CF交于点D，则下列结论中不正确的是(　　)

    A. △ABE≌△ACF B. 点D在∠BAC的平分线上

    C. △BDF≌△CDE D. D是BE的中点

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】[ 问题提出 ]

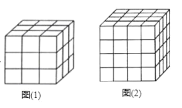
    一个边长为 ncm(n3)的正方体木块，在它的表面涂上颜色，然后切成边长为1cm的小正方体木块，没有涂上颜色的有多少块？只有一面涂上颜色的有多少块？有两面涂上颜色的有多少块？有三面涂上颜色的多少块？

    [ 问题探究 ]

    我们先从特殊的情况入手

    （1）当n=3时，如图（1）

    没有涂色的：把这个正方形的表层“剥去”剩下的正方体，有1×1×1=1个小正方体；

    一面涂色的：在面上，每个面上有1个，共有6个；

    两面涂色的：在棱上，每个棱上有1个，共有12个；

    三面涂色的：在顶点处，每个顶点处有1个，共有8个．

    （2）当n=4时，如图（2）

    没有涂色的：把这个正方形的表层“剥去”剩下的正方体，有2×2×2=8个小正方体：

    一面涂色的：在面上，每个面上有4个，正方体共有 个面，因此一面涂色的共有 个；

    两面涂色的：在棱上，每个棱上有2个，正方体共有 条棱，因此两面涂色的共有 个；

    三面涂色的：在顶点处，每个顶点处有1个，正方体共有 个顶点，因此三面涂色的共有 个…

    [ 问题解决 ]

    一个边长为ncm(n3)的正方体木块，没有涂色的：把这个正方形的表层“剥去”剩下的正方体，有______个小正方体；一面涂色的：在面上，共有______个； 两面涂色的：在棱上，共有______个； 三面涂色的：在顶点处，共______个。

    [ 问题应用 ]

    一个大的正方体，在它的表面涂上颜色，然后把它切成棱长1cm的小正方体，发现有两面涂色的小正方体有96个，请你求出这个大正方体的体积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直线y=﹣x+2与x轴、y轴分别交于点A、点C，抛物线经过点A、点C，且与x轴的另一个交点为B（﹣1，0）．

    （1）求抛物线的解析式；

    （2）点D为第一象限内抛物线上的一动点．

    ①如图1，若CD=AD，求点D的坐标；

    ②如图2，BD与AC交于点E，求S△CDE：S△CBE的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，PA、PB分别与⊙O相切于点A、B，若∠P=50°，则∠C的值是（ ）

    A. 50°B. 55°C. 60°D. 65°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个三位自然数m，将它任意两个数位上的数字对调后得一个首位不为0 的新三位自然数 m’（ m’可以与m相同），记m’=，在 m’ 所有的可能情况中，当|a+2b-c| 最小时，我们称此时的m’ 是m 的“幸福美满数”，并规定K (m) = a2 +2b2 -c2．例如：318按上述方法可得新数有：381、813 、138 ；因为|3+28－1｜＝ 18 ，｜8+ 21－3｜＝7，｜1 +23－8｜＝1，1< 7<18 ，所以138 是318的“幸福美满数”，K(318)=|12+232－82|=－45．

    （1）若三位自然数t的百位上的数字与十位上的数字都为n（1≤n ≤ 9 ，n为自然数），个位上的数字为0 ，求证：K (t )＝ 0；

    （2）设三位自然数s＝100+10x + y(1≤ x ≤ 9,1≤y≤9, ,x y 为自然数) ，且x<y ．交换其个位与十位上的数字得到新数s’，若19s+8s’=3888，那么我们称s为“梦

    想成真数”，求所有“梦想成真数”中K (s )的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】公园门票价格规定如下表：

    购票张数

    1~50张

    51~100张

    100张以上

    每张票的价格

    15元

    13元

    11元

    某校七年级(1)(2)两个班共102人去游园，其中(1)班超过40人，不足50人，经估算，如果两个班都以班为单位购票，则一共应付1422元.问：

    (1)两个班各有多少学生？

    (2)如果两个班联合起来，作为一个团体购票，可比两个班都以班为单位购票省多少元钱？

    (2)如果七年级(1)班单独组织去游园，作为组织者的你如何购票才最省钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，它表示甲乙两人从同一个地点出发后的情况。到10:00时，甲大约走了13千米。根据图象回答：

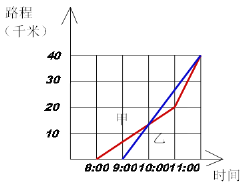
    （1）甲是几点钟出发？

    （2）乙是几点钟出发，到十点时，他大约走了多少千米？

    （3）到10:00为止，哪个人的速度快？

    （4）两人在途中有几次相遇？分别在几点钟相遇？

    查看答案和解析>>

    同步练习册答案