
如图,AB是☉O的直径,AM和BN是☉O的两条切线,E是☉O上一点,D是AM上一点,连接DE并延长交BN于点C,且OD∥BE,OF∥BN.

(1)求证:DE是☉O的切线.
(2)求证:OF = CD.
CD.
见解析
【解析】
试题分析:(1)连接OE,由AM与⊙O相切,利用切线的性质得到OA与AM垂直,即∠OAD=90°,根据
OD∥BE,利用两直线平行的性质得到一对内错角相等,一对同位角相等,再由OB=OE,利用等边对等角得到一对角相等,等量代换得到一对角相等,再由OA=OE,OD为公共边,利用SAS得出△AOD≌△EOD,利用全等三角形的性质:对应角相等得到∠OED=90°,即OE⊥ED,即可得证;
(2)连接OC,由CD与CB为圆的切线,利用切线的性质得到一对直角相等,由OB=OE,OC为公共边,利用HL得出两直角三角形全等,进而得到∠BOC=∠EOC,利用等量代换及平角定义得到∠COD=90°,即△COD为直角三角形,由OF∥BN,AM∥BN,得到三线平行,由O为AB的中点,利用平行线等分线段定理得到F为CD的中点,利用直角三角形斜边上的中线等于斜边的一半即可得证.
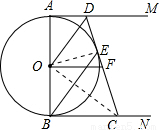
试题解析:(1)连接OE,AM是☉O的切线,OA是☉O的半径,
∴∠DAO=90°,
∵OD∥BE,
∴∠AOD=∠OBE,∠DOE=∠OEB,
∵OB=OE,
∴∠OEB=∠OBE.
∴∠AOD=∠DOE.
在△AOD和△DOE中

∴△AOD≌△EOD,
∴∠DAO=∠DEO=90°,
∴DE与☉O相切.
(2)∵AM和BN是☉O的两切线,
∴MA⊥AB,NB⊥AB,
∴AD∥BC,
∵O是AB的中点,OF∥BN,
∴OF∥AD且OF= (AD+BC).
(AD+BC).
∵DE切☉O于点E,
∴DA=DE,CB=CE,
∴DC=AD+CB,
∴OF= CD.
CD.
考点:切线的性质,平行线的性质与判定,全等三角形的性质与判定,平行线等分线段定理


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源:[同步]2014年北师大版八年级上 2.5用计算器开方练习卷(解析版) 题型:?????
使用课本所示型号的计算机,按键顺序是 ,最后显示的结果是( )
,最后显示的结果是( )
A.220 B.292 C.122 D.10
查看答案和解析>>
科目:初中数学 来源:[同步]2014年北师大版八年级上 2.4估算练习卷(解析版) 题型:?????
(2014•益阳)四个实数﹣2,0,﹣ ,1中,最大的实数是( )
,1中,最大的实数是( )
A.﹣2 B.0 C.﹣ D.1
D.1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省温州市五校联赛九年级实验B班1月联考数学试卷(解析版) 题型:选择题
如图,反比例函数 (
( <0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,
<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0, ),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则
),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则 的值是( )
的值是( )

A. B.
B. C.
C. D.
D.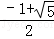
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省温州市五校联赛九年级实验B班1月联考数学试卷(解析版) 题型:选择题
若 在实数范围内有意义,则
在实数范围内有意义,则 的取值范围是( )
的取值范围是( )
A. B.
B.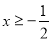 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期期中考试数学试卷(解析版) 题型:解答题
解方程:
(1)3(x﹣3)2+x(x﹣3)=0;
(2)x2﹣2x﹣3=0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,直线y= x﹣1与x轴交于点B,与双曲线y=
x﹣1与x轴交于点B,与双曲线y= (x>0)交于点A,过点B作x轴的垂线,与双曲线y=
(x>0)交于点A,过点B作x轴的垂线,与双曲线y= 交于点C,且AB=AC,则k的值为( )
交于点C,且AB=AC,则k的值为( )
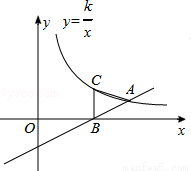
A.2 B.3 C.4 D.6
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期第三次阶段性测试数学试卷(解析版) 题型:解答题
(本题满分6分)如图△ABC中,DE∥BC, ,M为BC上一点,AM交DE于N.
,M为BC上一点,AM交DE于N.

(1)若AE=4,求EC的长;
(2)若M为BC的中点, =36,求
=36,求
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级12月月考数学试卷(解析版) 题型:填空题
若A(-4,yl),B(-3,y2),C(l,y3)为二次函数y=ax2+6ax-5 (a>0)的图象上的三点,则yl,y2,y3的大小关系是 .(用“<”号连接)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com