
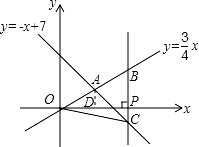
如图,在平面直角坐标系 xOy 中,已知正比例函数 y=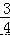 x 与一次函数 y=﹣x+7 的图象交于点 A.
x 与一次函数 y=﹣x+7 的图象交于点 A.
(1)求点 A 的坐标;
设 x 轴上有一点 P(a,0),过点 P 作 x 轴的垂线(垂线位于点 A 的右侧),分别交 y=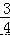 x 和 y=﹣x+7
x 和 y=﹣x+7
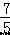 的图象于点 B、C,连接 OC.若 BC= OA,求△OBC 的面积.
的图象于点 B、C,连接 OC.若 BC= OA,求△OBC 的面积.
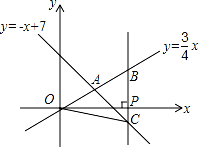
【考点】两条直线相交或平行问题;勾股定理.
【分析】(1)联立两一次函数的解析式求出 x、y 的值即可得出 A 点坐标;
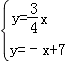 过点 A 作 x 轴的垂线,垂足为 D,在 Rt△OAD 中根据勾股定理求出 OA 的长,故可得出 BC 的长, 根据 P(a,0)可用 a 表示出 B、C 的坐标,故可得出 a 的值,由三角形的面积公式即可得出结论.
过点 A 作 x 轴的垂线,垂足为 D,在 Rt△OAD 中根据勾股定理求出 OA 的长,故可得出 BC 的长, 根据 P(a,0)可用 a 表示出 B、C 的坐标,故可得出 a 的值,由三角形的面积公式即可得出结论.
【解答】解:(1)∵由题意得, ,解得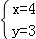 ,
,
∴A(4,3);
过点 A 作 x 轴的垂线,垂足为 D,在 Rt△OAD 中,由勾股定理得,
OA= 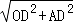 =
= 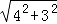 =5.
=5.
∴BC= 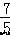 OA=
OA= 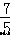 ×5=7.
×5=7.
∵P(a,0),
∴B(a,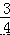 a),C(a,﹣a+7),
a),C(a,﹣a+7),
∴BC= 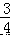 a﹣(﹣a+7)=
a﹣(﹣a+7)= 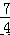 a﹣7,
a﹣7,
∴ 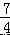 a﹣7=7,解得 a=8,
a﹣7=7,解得 a=8,
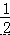
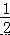 ∴S△OBC= BC•OP= ×7×8=28.
∴S△OBC= BC•OP= ×7×8=28.
【点评】本题考查的是两条直线相交或平行问题,根据题意作出辅助线.构造出直角三角形是解答 此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
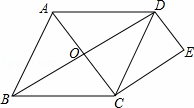
如图,已知菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
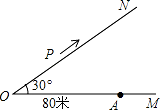
如图,有两条公路 OM、ON 相交成 30°角,沿公路 OM 方向离 O 点 80 米处有一所学校 A.当 重型运输卡车 P 沿道路 ON 方向行驶时,在以 P 为圆心 50 米长为半径的圆形区域内都会受到卡车噪 声的影响,且卡车 P 与学校 A 的距离越近噪声影响越大.若已知重型运输卡车 P 沿道路 ON 方向行 驶的速度为 18 千米/时.
(1)求对学校 A 的噪声影响最大时卡车 P 与学校 A 的距离; 求卡车 P 沿道路 ON 方向行驶一次给学校 A 带来噪声影响的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com