


科目:初中数学 来源: 题型:
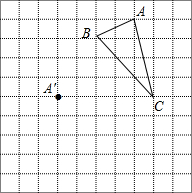 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A′,点B′、C′分别是B、C的对应点.查看答案和解析>>
科目:初中数学 来源: 题型:
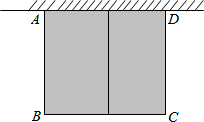 如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10米).如果AB的长为x,面积为y,
如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10米).如果AB的长为x,面积为y,查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、阴天一定会下雨 |
| B、在装有5个红球的袋中摸出1个球,是红球 |
| C、打开电视机,正在播放动画片 |
| D、某彩票中奖率是1%,买100张一定会中奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com