
【题目】在△ABC中,∠C=90°,AC=3,BC=4,△ABC外接圆⊙O的半径为 ,△ABC内切圆⊙I的半径为 .
【答案】(﹣2,﹣![]() )或(2,
)或(2,![]() ).
).
【解析】
试题分析:由勾股定理求出斜边AB,直角三角形外接圆的半径等于斜边的一半,即可得出△ABC外接圆⊙O的半径.由切线长定理得出AE=AD,CE=CF,BD=BF;证出四边形IECF是正方形,则列方程即可求得⊙I的半径r.
解:∵∠C=90°,AC=3,BC=4,
∴AB=![]() =5,
=5,
∴△ABC外接圆的半径为![]() AB=2.5;
AB=2.5;
连接△ABC内切圆⊙I的圆心I和各个切点,如图所示.
∵⊙I为△ABC的内切圆,
∴AE=AD,CE=CF,BD=BF,IE⊥AC,IF⊥BC,
∴∠IFC=∠IEC=∠C=90°,
∴四边形IECF是矩形;
∵IE=IF,
∴四边形IECF是正方形;
∵⊙I的半径为r,
∴CE=CF=r,AE=AD=3﹣r,BD=BF=4﹣r,
∴3﹣r+4﹣r=5,
解得:r=1,
∴△ABC的内切圆的半径r=1.
故答案为:2.5,1.



科目:初中数学 来源: 题型:
【题目】在直角三角形,两条直角边分别为6cm,8cm,斜边长为10cm,若分别以一边旋转一周(①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体=![]() ,V圆锥=
,V圆锥=![]() h)
h)
(1)如果绕着它的斜边所在的直线旋转一周形成的几何体是?
(2)如果绕着它的直角边6所在的直线旋转一周形成的几何体的体积是多少?
(3)如果绕着它的斜边10所在的直线旋转一周形成的几何体的体积与绕着直角边8所在的直线旋转一周形成的几何体的体积哪个大?
查看答案和解析>>
科目:初中数学 来源: 题型:
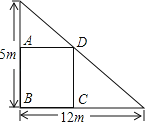
【题目】如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=xm,长方形的面积为ym2,要使长方形的面积最大,其边长x应为( )
A.![]() m B.6m C.25m D.
m B.6m C.25m D.![]() m
m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com