
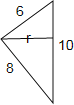
����Ŀ����ֱ�������Σ�����ֱ�DZ߷ֱ�Ϊ6cm��8cm��б�߳�Ϊ10cm�����ֱ���һ����תһ�ܣ������������ʾ����������õ����е�һ����ʽ��VԲ��=��r2h��V����=![]() ��VԲ=
��VԲ=![]() h��
h��
��1�������������б�����ڵ�ֱ����תһ���γɵļ������ǣ�
��2�������������ֱ�DZ�6���ڵ�ֱ����תһ���γɵļ����������Ƕ��٣�
��3�������������б��10���ڵ�ֱ����תһ���γɵļ���������������ֱ�DZ�8���ڵ�ֱ����תһ���γɵļ����������ĸ���
���𰸡���1������Բ�γɵļ����壻
��2��VԲ128����
��3������ֱ�DZ�8���ڵ�ֱ����תһ���γɵļ�����������
��������
�����������1����б���ϵĸ߷ֳ�����ֱ����������ת���ɣ�
��2��ȷ��Բ�ĸ���뾶������������
��3���ֱ��������ͼ�ε�������ٱȽϼ��ɣ�
�⣺��1������Բ�γɵļ����壻
��2��VԲ=![]() ��r2h=
��r2h=![]() ��82��6=128����
��82��6=128����
��3������ͼ![]() =
=![]() �����r=
�����r=![]() ��
��
��������б��10���ڵ�ֱ����תһ���γɵļ���������ΪVԲ=![]() ��r2h=
��r2h=![]() ����
����![]() ��2��10=76.8��
��2��10=76.8��
������ֱ�DZ�8���ڵ�ֱ����תһ���γɵļ���������ΪVԲ=![]() ��r2h=
��r2h=![]() ��62��8=96����
��62��8=96����
������ֱ�DZ�8���ڵ�ֱ����תһ���γɵļ�����������


 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е�ʽ��ȷ���ǣ� ��
A. -��3��=��-3�� B. ��3��=��-3��
C. ��-3��=-3 D. -�v-3�w=-��-3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧʵ���ң�
��A��B�������Ϸֱ��ʾ������a��b��A��B����֮��ľ����ʾΪAB����������A��B����֮��ľ���AB=|a��b|��
�������ν��˼��ش��������⣺
![]()
�������ϱ�ʾ2��5����֮��ľ����� �������ϱ�ʾ1����3������֮��ľ����� ��
�������ϱ�ʾx����2������֮��ľ����ʾΪ �������ϱ�ʾx��5������֮��ľ����ʾΪ ��
����x��ʾһ������������|x��1|+|x+3|����Сֵ= ��
����x��ʾһ������������|x+3|+|x��2|=5����������������������x���� ��
����x��ʾһ������������xΪ ��ʽ��|x+2|+|x��3|+|x��5|����СֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
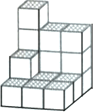
����Ŀ����ͼ����һ����ѧ����ϣ�������17���߳�Ϊ1��С�����δ����һ�������壬Ȼ����������������ͬ����С���������Ա��ٴ�һ�������壬ʹ�����������ǡ�ÿ��Ժ������������ƴ��һ����϶�Ĵ��壨���ı���������������״������ô�������ٻ���Ҫ ��С�����壬�����������ı����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���C=90����AC=3��BC=4����ABC���Բ��O�İ뾶Ϊ ����ABC����Բ��I�İ뾶Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶��ѧ��ȤС�龭���г����飬�õ�ij���˶���ÿ�µ��������ۼ۵������Ϣ�����
�ۼۣ�Ԫ/���� | 100 | 110 | 120 | 130 | �� |
������������ | 200 | 180 | 160 | 140 | �� |
��֪���˶����Ľ���Ϊÿ��60Ԫ�����ۼ�ΪxԪ��
��1����������m�����ۼ�xԪ/��֮��ĺ�������ʽ��
��2�������۸��˶�����������ΪyԪ��д��y��x֮��ĺ�������ʽ��������ۼ�xΪ����ʱ�����µ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��a��0��ͼ���һ���֣��Գ���Ϊx=![]() ���Ҿ����㣨2��0����������˵������abc��0����a+b=0����4a+2b+c��0��������0��y1������1��y2�����������ϵ����㣬��y1=y2������˵����ȷ���ǣ� ��
���Ҿ����㣨2��0����������˵������abc��0����a+b=0����4a+2b+c��0��������0��y1������1��y2�����������ϵ����㣬��y1=y2������˵����ȷ���ǣ� ��

A���٢ڢ� B���ۢ� C���٢ۢ� D���٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ���A=90������P��Q�ֱ���AB��AC�ϵ�һ���㣬������BP=AQ��D��BC���е㣮
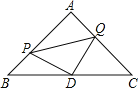
��1����֤����PDQ�ǵ���ֱ�������Σ�
��2������P�˶���ʲôλ��ʱ���ı���APDQ�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��82m��4n��2m��n
��2��6m362m��63m��2
��3����a4a3��a2��3
��4������10��2+����10��0+10��2������102��
��5����![]() x6y5+
x6y5+![]() x5y4��
x5y4��![]() x4y3����
x4y3����![]() x3y3
x3y3
��6��![]() x����2x��
x����2x��![]() y2��+��
y2��+��![]() x��
x��![]() y2��
y2��
��7��2��[x��![]() ��x��1��]��
��x��1��]��![]() ��x��1��
��x��1��
��8��5xy2��{2x2y��[3xy2����xy2��2x2y��]�£���![]() xy��}��
xy��}��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com