
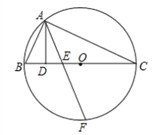
【题目】如图,△ABC内接于⊙O,且BC是⊙O的直径,AD⊥BC于D,F是弧BC中点,且AF交BC于E,连接OA,
(1)求证:AE平分∠DAO;
(2)若AB=6,AC=8,求OE的长.
【答案】(1)证明见解析;(2)OE=![]() .
.
【解析】试题分析:(1)连接OA,由BC是 O的直径,AD⊥BC,易得∠C=∠OAE=∠B,又由F是弧BC中点,可得∠BAF=∠CAF,继而证得AE平分∠DAO;
(2)首先连接OF,易得OF∥AD,即可得DE:OE=AD:OF,然后由勾股定理求得AD,BD的长,继而求得答案.
试题解析:
(1)证明:连接OA,
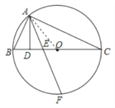
∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠C+∠B=90°,
∵AD⊥BC,
∴∠B+∠BAD=90°,
∴∠BAD=∠C,
∵OA=OC,
∴∠OAC=∠C,
∴∠BAD=∠OAC,
∵F是弧BC中点,
∴∠BAF=∠CAF,
∴∠DAE=∠OAE,
即AE平分∠DAO;
(2)解:连接OF,
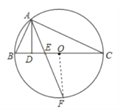
∵∠BOF=2∠BAF=∠BAC=90°,
∴OF⊥BC,
∵AD⊥BC,
∴OF∥AD,
∴DE:OE=AD:OF,
∵AB=6,AC=8,
∴BC=AB2+AC2=10,
∴AD=ABAC
BC=4.8,
∴BD=AB2AD2=3.6,
∴OD=OB-BD=5-3.6=1.4,
∴DE:OE=4.8:5=24:25,
∴OE=![]() .
.


科目:初中数学 来源: 题型:
【题目】边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
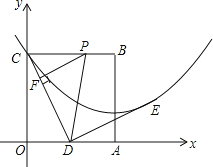
(1)求抛物线的解析式;
(2)点P从点C出发,沿射线CB每秒1个单位长度的速度运动,运动时间为t秒.过点P作PF⊥CD于点F,当t为何值时,以点P,F,D为顶点的三角形与△COD相似?
(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
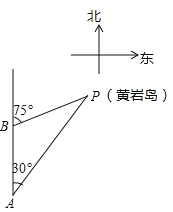
【题目】如图,三沙市一艘海监船某天在黄岩鸟P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据: ![]() ≈1.414,结果精确到0.1)
≈1.414,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M,N分别是射线AE,AF上的点,且PM=PN. 
(1)如图1,当点M在线段AB上,点N在线段AC的延长线上时,求证:BM=CN;
(2)在(1)的条件下,直接写出线段AM,AN与AC之间的数量关系;
(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,若AC:PC=2:1,且PC=4,求四边形ANPM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,
, ![]() 在数轴上对应的实数分别是
在数轴上对应的实数分别是![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 满足
满足![]() .
.
(![]() )求线段
)求线段![]() 的长.
的长.
(![]() )点
)点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,且
,且![]() 是方程
是方程![]() 的解,在数轴上是否存在点
的解,在数轴上是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 对应的数;若不存在,说明理由.
对应的数;若不存在,说明理由.
(![]() )在(
)在(![]() )和(
)和(![]() )的条件下,点
)的条件下,点![]() ,
, ![]() ,
, ![]() 同时开始在数轴上运动,若点
同时开始在数轴上运动,若点![]() 以每秒
以每秒![]() 个单位长度是速度向左运动,点
个单位长度是速度向左运动,点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动,点
个单位长度的速度向右运动,点![]() 与点
与点![]() 之间距离表示为
之间距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .设运动时间为
.设运动时间为![]() 秒,试探究,随着时间
秒,试探究,随着时间![]() 的变化,
的变化, ![]() 与
与![]() 满足怎样的数量关系?请写出相应的等式.
满足怎样的数量关系?请写出相应的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是2015年12月月历.
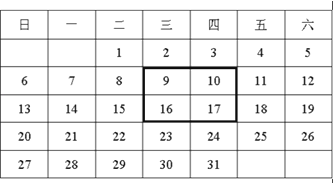
(1)如图,用一正方形框在表中任意框住4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是 , , .
(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2= .
(3)当(1)中被框住的4个数之和等于76时,x的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB:y=﹣ ![]() x+5与x轴、y轴分别交于点A、B,y轴上点C的坐标为(0,10).
x+5与x轴、y轴分别交于点A、B,y轴上点C的坐标为(0,10).
(1)求A、B两点的坐标;
(2)动点M从A点出发,以每秒1个单位长度的速度,沿x轴向左运动,连接CM.设点M的运动时间为t,△COM的面积为S,求S与t的函数关系式;(并标出自变量的取值范围)
(3)直线AB与直线CM相交于点N,点P为y轴上一点,且始终保持PM+PN最短,当t为何值时,△COM≌△AOB,并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一组有规律的数:1,﹣1, ![]() ,﹣
,﹣ ![]() ,
, ![]() ,﹣
,﹣ ![]() ,1,﹣1,
,1,﹣1, ![]() ,﹣
,﹣ ![]() ,
, ![]() ,﹣
,﹣ ![]() …其中1,﹣1,
…其中1,﹣1, ![]() ,﹣
,﹣ ![]() ,
, ![]() ,﹣
,﹣ ![]() 这六个数按此规律重复出现.
这六个数按此规律重复出现.
(1)第50个数是什么数?
(2)把从第1个数开始的前2017个数相加,结果是多少?
(3)从第1个数起,把连续若干个数的平方相加起来,如果和为520,那么一共是多少和数的平方相加?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com