
【题目】在![]() 中,
中,![]() ,
,![]() ,以点
,以点![]() 为圆心、
为圆心、![]() 为半径作圆,设点
为半径作圆,设点![]() 为⊙
为⊙![]() 上一点,线段
上一点,线段![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() 、
、![]() .
.
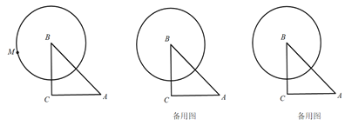
(1)在图中,补全图形,并证明![]() .
.
(2)连接![]() ,若
,若![]() 与⊙
与⊙![]() 相切,则
相切,则![]() 的度数为 .
的度数为 .
(3)连接![]() ,则
,则![]() 的最小值为 ;
的最小值为 ;![]() 的最大值为 .
的最大值为 .
【答案】(1)证明见解析;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)根据题意,作出图像,然后利用SAS证明![]() ,即可得到结论;
,即可得到结论;
(2)根据题意,由![]() 与⊙
与⊙![]() 相切,得到∠BMN=90°,结合点M的位置,即可求出
相切,得到∠BMN=90°,结合点M的位置,即可求出![]() 的度数;
的度数;
(3)根据题意,当点N恰好落在线段AB上时,BN的值最小;当点N落在BA延长线上时,BN的值最大,分别求出BN的值,即可得到答案.
解:(1)如图,补全图形,
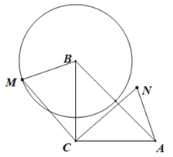
证明:![]()
![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ;
;
(2)根据题意,连接MN,
∵![]() 与⊙
与⊙![]() 相切,
相切,
∴∠BMN=90°,
∵△MNC是等腰直角三角形,
∴∠CMN=45°,
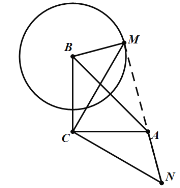
如上图所示,∠BMC=![]() ;
;
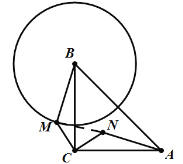
如上图所示,∠BMC=![]() ;
;
综合上述,![]() 的度数为:
的度数为:![]() 或
或![]() ;
;
故答案为:![]() 或
或![]() ;
;
(3)根据题意,当点N恰好落在线段AB上时,BN的值最小;如图所示,
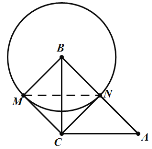
∵AN=BM=1,
∵![]() ,
,
∴![]() ;
;
当点N落在BA延长线上时,BN的值最大,如图所示,
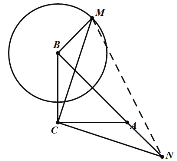
由AN=BN=1,
∴BN=BA+AN=2+1=3;
∴![]() 的最小值为1;
的最小值为1;![]() 的最大值为3;
的最大值为3;
故答案为:1,3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
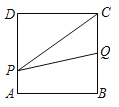
【题目】如图,边长为2的正方形ABCD,点P从点A出发以每秒1个单位长度的速度沿A﹣D﹣C的路径向点C运动,同时点Q从点B出发以每秒2个单位长度的速度沿B﹣C﹣D﹣A的路径向点A运动,当Q到达终点时,P停止移动,设△PQC的面积为S,运动时间为t秒,则能大致反映S与t的函数关系的图象是( )
A.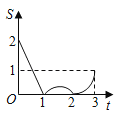 B.
B.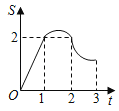
C.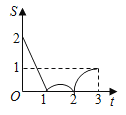 D.
D.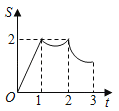
查看答案和解析>>
科目:初中数学 来源: 题型:
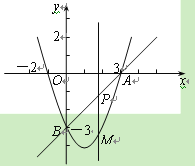
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、
B(0,-3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横
坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,其中图象与
的部分图象如图所示,其中图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() .
.

![]() 求此二次函数的解析式;
求此二次函数的解析式;
![]() 将此二次函数的解析式写成
将此二次函数的解析式写成![]() 的形式,并直接写出顶点坐标以及它与
的形式,并直接写出顶点坐标以及它与![]() 轴的另一个交点
轴的另一个交点![]() 的坐标.
的坐标.
![]() 利用以上信息解答下列问题:若关于
利用以上信息解答下列问题:若关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() 为实数)在
为实数)在![]() 的范围内有解,则
的范围内有解,则![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个二次函数图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如下表所示:
的对应值如下表所示:
| ... |
|
|
|
|
| ... |
| ... |
|
|
|
|
| ... |
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
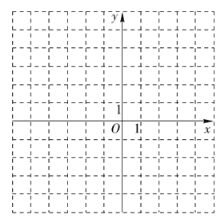
(3![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材呈现:下图是华师版九年级上册数学教材第77页的部分内容.
猜想
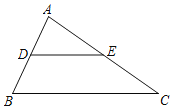
如图,在△ABC中,点D、E分别是AB与AC的中点,根据画出的图形,可以猜想:
DE∥BC,且DE=![]() BC.
BC.
对此,我们可以用演绎推理给出证明
证明在△ABC中,
∵点D、E分别是AB与AC的中点,
∴![]() 请根据教材提示,结合图①,写出完整证明过程,
请根据教材提示,结合图①,写出完整证明过程,
结论应用:
如图②在四边形ABCD中,AD=BC,点P是对角线BD的中点,M是DC中点,N是AB中点,MN与BD相交于点Q.
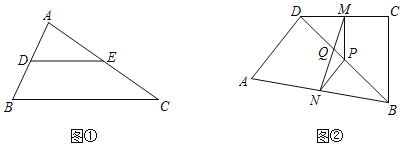
(1)求证:∠PMN=∠PNM;
(2)若AD=BC=4,∠ADB=90°,∠DBC=30°,则PQ= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,y是关于
,y是关于![]() 的二次函数,抛物线
的二次函数,抛物线![]() 经过点
经过点![]() .抛物线
.抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 则下列判断:
则下列判断:
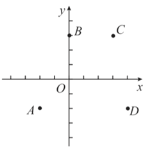
①四条抛物线的开口方向均向下;
②当![]() 时,四条抛物线表达式中的
时,四条抛物线表达式中的![]() 均随
均随![]() 的增大而增大;
的增大而增大;
③抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 顶点的上方;
顶点的上方;
④抛物线![]() 与
与![]() 轴交点在点
轴交点在点![]() 的上方.
的上方.
其中正确的是
A.①②④B.①③④
C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点A、B(点A在点B的左侧),且AB=6.
轴交于点A、B(点A在点B的左侧),且AB=6.
(1)求这条抛物线的对称轴及表达式;
(2)在y轴上取点E(0,2),点F为第一象限内抛物线上一点,联结BF、EF,如果![]() ,求点F的坐标;
,求点F的坐标;
(3)在第(2)小题的条件下,点F在抛物线对称轴右侧,点P在![]() 轴上且在点B左侧,如果直线PF与y轴的夹角等于∠EBF,求点P的坐标.
轴上且在点B左侧,如果直线PF与y轴的夹角等于∠EBF,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校旗杆的下方有一块圆形草坪,草坪的外面围着“圆环”水池,草坪和水池的外边缘是两个同心圆,旗杆在圆心O的位置且与地面垂直.
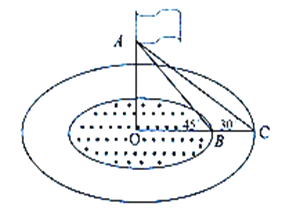
(1)若草坪的面积与圆环水池的面积之比为1∶4,求两个同心圆的半径之比.
(2)如图,若水池外面通往草坪有一座10米长的小桥BC,小桥所在的直线经过圆心O,上午8:00时太阳光线与地面成30°角,旗杆顶端的影子恰好落在水池的外缘;上午9:00时太阳光线与地面成45°角,旗杆顶端的影子恰好落在草坪的外缘,求旗杆的高OA长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com