
����Ŀ������˵�������߲���������ÿ������ʱ�֣�����в����˱����˯������˯�Ѻ��ѣ����ǿ�������ʳ������з��Σ���������ʳ��ɷ��δ������㴻�����⡢�²ˡ�ɽҩ����Ƭ�����켴������ʱ��ij����ץס�̻��������ס��ҡ���������Ƭ����֪����ÿ��������Ƭ��������Ϊ10%��ÿ��������Ƭ��������Ϊ20%��ÿ��������Ƭ��������Ϊ30%�����۳��ļס��ҡ���������Ƭ�Ĵ���֮��Ϊ1��3��1ʱ�����˵õ�����������Ϊ22%�����۳��ļס��ҡ������ֱ�Ƭ�Ĵ���֮��Ϊ3��2��1ʱ�����˵õ�����������Ϊ20%����ô���۳��ļס��ҡ���������Ƭ�Ĵ���֮��Ϊ2��3��4ʱ��������˵õ�����������Ϊ_____���ðٷֺű����ս������
���𰸡�25%��
��������
��ס��ҡ������ַ��۵Ľ��۷ֱ�Ϊa��b��c���������۳�ƿ��Ϊcx�����۳��ļס��ҡ�������ƿ��֮��Ϊ1��3��1ʱ���ס��ҷ����۳�ƿ���ֱ�Ϊax��3bx�����۳��ļס��ҡ�������ƿ��֮��Ϊ3��2��1ʱ���ס��ҷ����۳�ƿ���ֱ�Ϊ3ax��2bx���г����̣��ⷽ�����![]() �����ɵó������
�����ɵó������
�⣺��ס��ҡ���������Ƭ�Ľ��۷ֱ�Ϊa��b��c������Ƭ�۳�����Ϊcx��
������ã�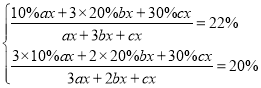 ��
��
��ã�![]() ��
��
��![]() ��
��
�ʴ�Ϊ��25%��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
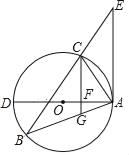
����Ŀ����ͼ����O�ǡ�ABC�����Բ�� AD�ǡ�O��ֱ����BC���ӳ����ڹ���A��ֱ���ཻ�ڵ�E���ҡ�B=��EAC��
��1����֤��AE�ǡ�O�����ߣ�
��2������C��CG��AD������ΪF����AB���ڵ�G����AGAB=36��tanB=![]() ����DF��ֵ
����DF��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
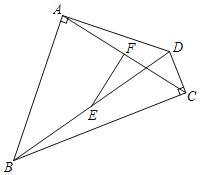
����Ŀ����ͼ���ı���ABCD�У���BAD��90�㣬��DCB��90�㣬E��F�ֱ���BD��AC���е㣮
��1���������EF��AC��λ�ù�ϵ��������֤����
��2����AC��16��BD��20ʱ����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ֽƬABCD�۵���ʹ��DC���ڶԽ���AC�ϣ��ۺ�ΪCE����D�����ڶԽ���D��������AB=3��AD=4����ED�ij�Ϊ

A��![]() B��3 C��1 D��
B��3 C��1 D��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
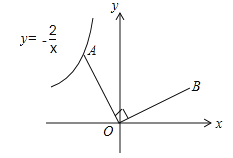
����Ŀ����ͼ����֪��A�Ƿ���������![]() ��ͼ���ϵ�һ�����㣬����OA�������߶�O A�Ƶ�O˳ʱ����ת90��õ��߶�OB�����B����ͼ��ĺ�������ʽΪ______��
��ͼ���ϵ�һ�����㣬����OA�������߶�O A�Ƶ�O˳ʱ����ת90��õ��߶�OB�����B����ͼ��ĺ�������ʽΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��l1��y��x+5�뷴��������y��![]() ��k��0��x��0��ͼ���ڵ�A��1��n������һ��ֱ��l2��y����2x+b��x�ύ�ڵ�E����y�ύ�ڵ�B���뷴��������y��
��k��0��x��0��ͼ���ڵ�A��1��n������һ��ֱ��l2��y����2x+b��x�ύ�ڵ�E����y�ύ�ڵ�B���뷴��������y��![]() ��k��0��x��0��ͼ���ڵ�C�͵�D��
��k��0��x��0��ͼ���ڵ�C�͵�D��![]() ��m��������OC��OD��
��m��������OC��OD��
��1��������������ʽ�͵�C�����ꣻ
��2�����OCD�������
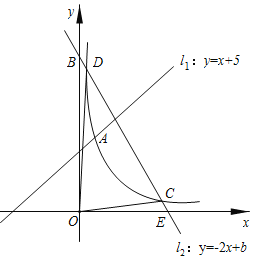
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
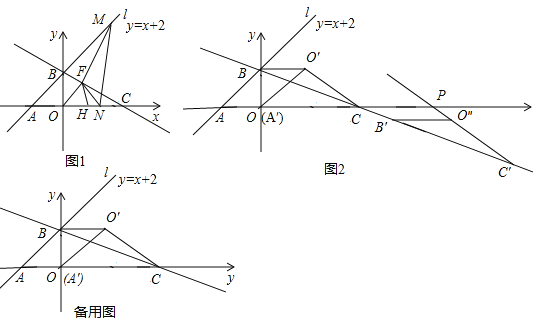
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��l��y��x+2��x�ύ�ڵ�A����y�ύ�ڵ�B����C��x����������ϣ���OC��2OB��
��1����F��ֱ��BC��һ���㣬��M��ֱ��AB��һ���㣬��HΪx����һ���㣬��NΪx������һ���㣨����H���غϣ�������OF��FH��FM��FN��MN����OF+FHȡ��Сֵʱ�����FMN�ܳ�����Сֵ��
��2����ͼ2������AOB���ŵ�B��ʱ����ת90��õ���A��O��B�����е�A��Ӧ��ΪA�䣬��O��Ӧ��ΪO'������CO'������BCO'����ֱ��BCƽ�ƣ���ƽ�ƹ����С�BCO'Ϊ��B'C'O�壬���е�B��Ӧ��ΪB'����C��Ӧ��ΪC'����O���Ӧ��ΪO�壬ֱ��C'O����x�ύ�ڵ�P����ƽ�ƹ����У��Ƿ���ڵ�P��ʹ�á�O��PCΪ���������Σ���������ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
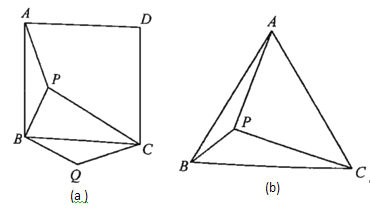
����Ŀ����1����ͼ��a����ʾ����![]() ��������
��������![]() �ڵ�һ�㣬��
�ڵ�һ�㣬��![]() �Ƶ�
�Ƶ�![]() ˳ʱ�뷽����ת��ʹ��
˳ʱ�뷽����ת��ʹ��![]() ���
���![]() �غϣ���
�غϣ���![]() �Ķ�Ӧ����
�Ķ�Ӧ����![]() ����
����![]() ��
��![]() ��
��![]() ����
����![]() �Ķ�����
�Ķ�����
��2����ͼ��b����ʾ����![]() �ǵȱ�������
�ǵȱ�������![]() �ڵ�һ�㣬��
�ڵ�һ�㣬��![]() ��
��![]() ��
��![]() ����
����![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊ������Ӫ����������6̨������������ij���������мס������ֻ�����ѡ������ÿ�ֻ����ļ۸��ÿ̨�����������������������±���ʾ������Ԥ�㣬���ι�����������ʽ��ܳ���34��Ԫ.
�� | �� | |
�۸�(��Ԫ/̨) | 7 | 5 |
ÿ̨�ղ���(��) | 100 | 60 |
(1)���ù�˾Ҫ������м��ֹ�����
(2)����ù�˾������6̨�������������������ܵ���380������ôΪ�˽�Լ�ʽ�Ӧѡ��ʲô���Ĺ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com