
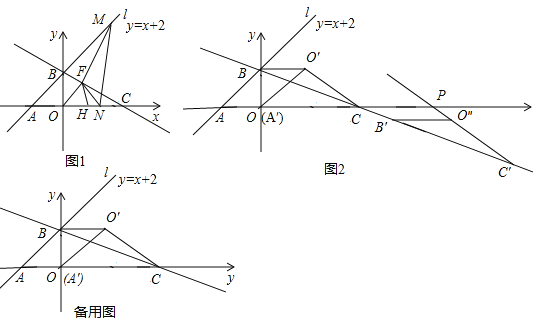
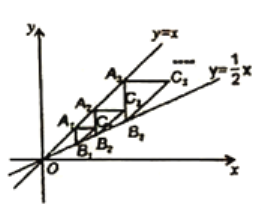
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпlЃКyЃНx+2гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌЕуCдкxжсЕФе§АыжсЩЯЃЌЧвOCЃН2OBЃЎ
ЃЈ1ЃЉЕуFЪЧжБЯпBCЩЯвЛЖЏЕуЃЌЕуMЪЧжБЯпABЩЯвЛЖЏЕуЃЌЕуHЮЊxжсЩЯвЛЖЏЕуЃЌЕуNЮЊxжсЩЯСэвЛЖЏЕуЃЈВЛгыHЕужиКЯЃЉЃЌСЌНгOFЁЂFHЁЂFMЁЂFNКЭMNЃЌЕБOF+FHШЁзюаЁжЕЪБЃЌЧѓЁїFMNжмГЄЕФзюаЁжЕЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌНЋЁїAOBШЦзХЕуBФцЪБеыа§зЊ90ЁуЕУЕНЁїAЁфOЁфBЃЌЦфжаЕуAЖдгІЕуЮЊAЁфЃЌЕуOЖдгІЕуЮЊO'ЃЌСЌНгCO'ЃЌНЋЁїBCO'бизХжБЯпBCЦНвЦЃЌМЧЦНвЦЙ§ГЬжаЁїBCO'ЮЊЁїB'C'OЁхЃЌЦфжаЕуBЖдгІЕуЮЊB'ЃЌЕуCЖдгІЕуЮЊC'ЃЌЕуOЁфЖдгІЕуЮЊOЁхЃЌжБЯпC'OЁхгыxжсНЛгкЕуPЃЌдкЦНвЦЙ§ГЬжаЃЌЪЧЗёДцдкЕуPЃЌЪЙЕУЁїOЁхPCЮЊЕШбќШ§НЧаЮЃПШєДцдкЧыжБНгаДГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉТњзуЬѕМўЕФЕуPЮЊЃКЃЈ8+2
ЃЛЃЈ2ЃЉТњзуЬѕМўЕФЕуPЮЊЃКЃЈ8+2![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ5ЃЌ0ЃЉ
ЃЌ0ЃЉЛђЃЈ5ЃЌ0ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіЕуAЃЌЕуBзјБъЃЌгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпBCЕФНтЮіЪНЃЌзїЕуOЙигкжБЯпBCЕФЖдГЦЕуO'ЃЈ![]() ЃЉЃЌЙ§ЕуO'зїO'HЁЭOCгкЕуFЃЌНЛBCгкЕуHЃЌДЫЪБOF+FHЕФжЕзюаЁЃЌЧѓГіЕуFзјБъЃЌзїЕуFЙигкжБЯпABгыжБЯпOCЕФЖдГЦЕуЃЌСЌНгF'F'НЛжБЯпABгкЕуMЃЌНЛжБЯпOCгкЕуNЃЌДЫЪБЁїFMNжмГЄгазюаЁжЕЃЌгЩСНЕуОрРыЙЋЪНПЩЧѓЁїFMNжмГЄЕФзюаЁжЕЃЛ
ЃЉЃЌЙ§ЕуO'зїO'HЁЭOCгкЕуFЃЌНЛBCгкЕуHЃЌДЫЪБOF+FHЕФжЕзюаЁЃЌЧѓГіЕуFзјБъЃЌзїЕуFЙигкжБЯпABгыжБЯпOCЕФЖдГЦЕуЃЌСЌНгF'F'НЛжБЯпABгкЕуMЃЌНЛжБЯпOCгкЕуNЃЌДЫЪБЁїFMNжмГЄгазюаЁжЕЃЌгЩСНЕуОрРыЙЋЪНПЩЧѓЁїFMNжмГЄЕФзюаЁжЕЃЛ
ЃЈ2ЃЉЗжO'CЃНPCЃЌO'PЃНPCЃЌO'PЃНO'CШ§жжЧщПіЬжТлЃЌгЩЕШбќШ§НЧаЮЕФаджЪПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉЁпжБЯпyЃНx+2гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌ
ЁрЕБxЃН0ЪБЃЌyЃН2ЃЌ
ЕБyЃН0ЪБЃЌxЃНЉ2ЃЌ
ЁрЕуAЃЈЉ2ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌ2ЃЉ
ЁрOBЃН2
ЁпOCЃН2OBЃЎ
ЁрOCЃН4
ЁрЕуCЃЈ4ЃЌ0ЃЉ
ЩшжБЯпBCНтЮіЪНЮЊЃКyЃНkx+2ЃЌЧвЙ§ЕуCЃЈ4ЃЌ0ЃЉ
Ёр0ЃН4k+2
ЁрkЃН![]()
ЁржБЯпBCНтЮіЪНЮЊЃКyЃН![]() x+2ЃЌ
x+2ЃЌ
ШчЭМЃЌзїЕуOЙигкжБЯпBCЕФЖдГЦЕуO'ЃЈ![]() ЃЉЃЌЙ§ЕуO'зїO'HЁЭOCгкЕуFЃЌНЛBCгкЕуHЃЌДЫЪБOF+FHЕФжЕзюаЁЃЎ
ЃЉЃЌЙ§ЕуO'зїO'HЁЭOCгкЕуFЃЌНЛBCгкЕуHЃЌДЫЪБOF+FHЕФжЕзюаЁЃЎ
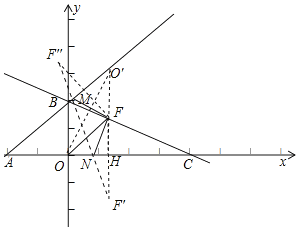
ЁрЕуFЕФКсзјБъЮЊ![]()
ЁрЕуFЃЈ![]() ЃЉ
ЃЉ
зїЕуFЙигкжБЯпOCЕФЖдГЦЕуF'ЃЈ![]() ЃЉЃЌ
ЃЉЃЌ
зїЕуFЙигкжБЯпABЕФЖдГЦЕуF'ЃЈ![]() ЃЉ
ЃЉ
СЌНгF'F'НЛжБЯпABгкЕуMЃЌНЛжБЯпOCгкЕуNЃЌДЫЪБЁїFMNжмГЄгазюаЁжЕЃЌ
ЁрЁїFMNжмГЄЕФзюаЁжЕЃН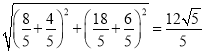
ЃЈ2ЃЉЁпНЋЁїAOBШЦзХЕуBФцЪБеыа§зЊ90ЁуЕУЕНЁїA'OЁЏBЃЌ
ЁрO'ЕузјБъЃЈ2ЃЌ2ЃЉ
ЩшжБЯпO'CЕФНтЮіЪНЮЊЃКyЃНmx+b
Ёр![]()
Ёр![]()
ЁржБЯпO'CЕФНтЮіЪНЮЊЃКyЃНЉx+4
ШчЭМЃЌЙ§ЕуO'зїO'EЁЭOC
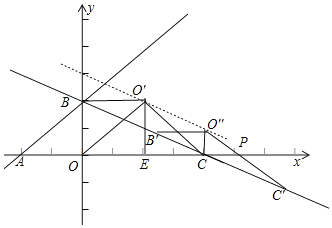
ЁрOEЃН2ЃЌO'EЃН2
ЁрECЃНO'EЃН2
ЁрЁЯO'CEЃН45Ёу
ЁпНЋЁїBCO'бизХжБЯпBCЦНвЦЃЌ
ЁрO'O'ЁЮBCЃЌO'CЁЮO'C'ЃЌ
ЁрЩшO'O'ЕФНтЮіЪНЮЊyЃН![]() x+nЃЌЧвЙ§ЃЈ2ЃЌ2ЃЉ
x+nЃЌЧвЙ§ЃЈ2ЃЌ2ЃЉ
Ёр2ЃН![]() ЁС2+n
ЁС2+n
ЁрnЃН3
ЁржБЯпO'O'ЕФНтЮіЪНЮЊyЃН![]() x+3
x+3
ШєCO'ЃНCPЃЌ
ЁпO'CЁЮO'C'ЃЌ
ЁрЁЯO'CEЃНЁЯO'PCЃН45Ёу
ЁпCO'ЃНCP
ЁрЁЯCO'PЃНЁЯO'PCЃН45Ёу
ЁрЁЯO'CPЃН90Ёу
ЁрЕуO'ЕФКсзјБъЮЊ4ЃЌ
ЁрЕБxЃН4ЪБЃЌyЃН![]() ЁС4+3ЃН1
ЁС4+3ЃН1
ЁрЕуO'ЃЈ4ЃЌ1ЃЉ
ЁрCO'ЃН1ЃНCP
ЁрЕуPЃЈ5ЃЌ0ЃЉ
ШєCO'ЃНO'PЃЌШчЭМЃЌЙ§ЕуO'зїO'NЁЭCPгкNЃЌ

ЁпO'CЁЮO'C'ЃЌ
ЁрЁЯO'CEЃНЁЯO'PCЃН45Ёу
ЁпCO'ЃНO'P
ЁрЁЯO'CPЃНЁЯCPO'ЃН45ЁуЃЌ
ЁрЁЯCO'PЃН90ЁуЃЌЧвCO'ЃНO'PЃЌO'NЁЭCP
ЁрCNЃНPNЃНO'NЃН![]() CP
CP
ЩшCPЃНaЃЌ
ЁрCNЃНPNЃНO'NЃН![]() CPЃН
CPЃН![]() a
a
ЁрЕуO'ЃЈ4+![]() aЃЌ
aЃЌ![]() aЃЉЃЌЧвжБЯпO'O'ЕФНтЮіЪНЮЊyЃНЉ
aЃЉЃЌЧвжБЯпO'O'ЕФНтЮіЪНЮЊyЃНЉ![]() x+3
x+3
Ёр![]() aЃНЉ
aЃНЉ![]() ЃЈ4+
ЃЈ4+![]() aЃЉ+3
aЃЉ+3
ЁрaЃН![]()
ЁрCPЃН![]()
ЁрЕуPЃЈ![]() ЃЌ0ЃЉ
ЃЌ0ЃЉ
ШєCPЃНO'PЃЌШчЭМЃЌЙ§ЕуO'зїO'NЁЭCPгкN

ЁпO'CЁЮO'C'ЃЌ
ЁрЁЯO'CEЃНЁЯO'PMЃН45Ёу
ЁрЁЯO'PNЃНЁЯO'PMЃН45ЁуЃЌЧвO'NЁЭCP
ЁрЁЯNPO'ЃНЁЯPO'NЃН45Ёу
ЁрPNЃНO'N
ЁрO'PЃН![]() PNЃНCP
PNЃНCP
ЩшPNЃНbЃЌдђO'NЃНbЃЌCPЃНPO'ЃН![]() b
b
ЁрЕуO'зјБъЃЈ4+![]() b+bЃЌЉbЃЉЃЌЧвжБЯпO'O'ЕФНтЮіЪНЮЊyЃН
b+bЃЌЉbЃЉЃЌЧвжБЯпO'O'ЕФНтЮіЪНЮЊyЃН![]() x+3
x+3
ЁрЉbЃН![]() ЁСЃЈ4+
ЁСЃЈ4+![]() b+bЃЉ+3
b+bЃЉ+3
ЁрbЃН2![]() +2
+2
ЁрCPЃН4+2![]()
ЁрЕуPзјБъЃЈ8+2![]() ЃЌ0ЃЉ
ЃЌ0ЃЉ
злЩЯЫљЪіЃКТњзуЬѕМўЕФЕуPЮЊЃКЃЈ8+2![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ5ЃЌ0ЃЉ
ЃЌ0ЃЉЛђЃЈ5ЃЌ0ЃЉ


 аТПЮБъНзЬндФЖСбЕСЗЯЕСаД№АИ
аТПЮБъНзЬндФЖСбЕСЗЯЕСаД№АИ ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ
ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЙ§Еу
ЩЯЃЌЙ§Еу![]() зї
зї![]() жсНЛжБЯп
жсНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌвдЕу
ЃЌвдЕу![]() ЮЊжБНЧЖЅЕуЃЌ
ЮЊжБНЧЖЅЕуЃЌ![]() ЮЊжБНЧБпдк
ЮЊжБНЧБпдк![]() ЕФгвВрзїЕШбќжБНЧ
ЕФгвВрзїЕШбќжБНЧ![]() ЃЌдйЙ§Еу
ЃЌдйЙ§Еу![]() зї
зї![]() жсЃЌЗжБ№НЛжБЯп
жсЃЌЗжБ№НЛжБЯп![]() КЭ
КЭ![]() гк
гк![]() ЃЌ
ЃЌ![]() СНЕуЃЌвдЕу
СНЕуЃЌвдЕу![]() ЮЊжБНЧЖЅЕуЃЌ
ЮЊжБНЧЖЅЕуЃЌ![]() ЮЊжБНЧБпдк
ЮЊжБНЧБпдк![]() ЕФгвВрзїЕШбќжБНЧ
ЕФгвВрзїЕШбќжБНЧ![]() АДДЫЙцТЩНјааЯТШЅЃЌдђЕШбќжБНЧ
АДДЫЙцТЩНјааЯТШЅЃЌдђЕШбќжБНЧ![]() ЕФУцЛ§ЮЊ_______ЃЌЕШбќжБНЧ
ЕФУцЛ§ЮЊ_______ЃЌЕШбќжБНЧ![]() ЕФУцЛ§ЮЊ______ЃЎ
ЕФУцЛ§ЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
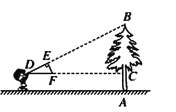
ЁОЬтФПЁПШчЭМЃЌаЁУїЭЌбЇгУзджЦЕФжБНЧШ§НЧаЮжНАхDEFВтСПЪїABЕФИпЖШЃЌЫћЕїећздМКЕФЮЛжУЃЌЩшЗЈЪЙаББпDFБЃГжЫЎЦНЃЌВЂЧвБпDEгыЕуBдкЭЌвЛжБЯпЩЯЃЌвбжЊжНАхЕФСНЬѕжБНЧБпDEЃН40cmЃЌEFЃН20cmЃЌВтЕУБпDFРыЕиУцЕФИпЖШACЃН1.5mЃЌCDЃН8mЃЌЧѓЪїABЕФИпЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙХгяЫЕЃКЁАДКУпВЛОѕЯўЁБЃЌУПЕНГѕДКЪБЗжЃЌЯыБигаВЛЩйШЫБфЕУЪШЫЏЃЌЖјЧвЫЏабКѓОЋЩёВЛМбЃЎЮвУЧПЩвддквћЪГЗНУцНјааЗРжЮЃЌБШШчвдЯТЪГЮяПЩЗРжЮДКРЇЃКЯуДЛЁЂДѓЫтЁЂОТВЫЁЂЩНвЉЁЂТѓЦЌЃЎДКЬьМДНЋРДСйЪБЃЌФГЩЬШЫзЅзЁЩЬЛњЃЌЙКНјМзЁЂввЁЂБћШ§жжТѓЦЌЃЌвбжЊЯњЪлУПДќМзжжТѓЦЌЕФРћШѓТЪЮЊ10%ЃЌУПДќввжжТѓЦЌЕФРћШѓТЪЮЊ20%ЃЌУПДќБћжжТѓЦЌЕФРћШѓТЪЮЊ30%ЃЌЕБЪлГіЕФМзЁЂввЁЂБћШ§жжТѓЦЌЕФДќЪ§жЎБШЮЊ1ЃК3ЃК1ЪБЃЌЩЬШЫЕУЕНЕФзмРћШѓТЪЮЊ22%ЃЛЕБЪлГіЕФМзЁЂввЁЂБћШ§жжБфЦЌЕФДќЪ§жЎБШЮЊ3ЃК2ЃК1ЪБЃЌЩЬШЫЕУЕНЕФзмРћШѓТЪЮЊ20%ЃКФЧУДЕБЪлГіЕФМзЁЂввЁЂБћШ§жжТѓЦЌЕФДќЪ§жЎБШЮЊ2ЃК3ЃЛ4ЪБЃЌетИіЩЬШЫЕУЕНЕФзмРћШѓТЪЮЊ_____ЃЈгУАйЗжКХБэзюжеНсЙћЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУA4жНИДгЁЮФМўЃЌдкМзИДгЁЕъВЛЙмвЛДЮИДгЁЖрЩйвГЃЌУПвГЪеЗб0.1дЊЃЎдкввИДгЁЕъИДгЁЭЌбљЕФЮФМўЃЌвЛДЮИДгЁвГЪ§ВЛГЌЙ§20ЪБЃЌУПвГЪеЗб0.12дЊЃЛвЛДЮИДгЁвГЪ§ГЌЙ§20ЪБЃЌГЌЙ§ВПЗжУПвГЪеЗб0.09дЊЃЎ
ЩшдкЭЌвЛМвИДгЁЕъвЛДЮИДгЁЮФМўЕФвГЪ§ЮЊx(xЮЊЗЧИКећЪ§)ЃЎ
(1)ИљОнЬтвтЃЌЬюаДЯТБэЃК
вЛДЮИДгЁвГЪ§(вГ) | 5 | 10 | 20 | 30 | Ё |
МзИДгЁЕъЪеЗб(дЊ) | 0.5 | ЁЁ ЁЁ | 2 | ЁЁ ЁЁ | Ё |
ввИДгЁЕъЪеЗб(дЊ) | 0.6 | ЁЁ ЁЁ | 2.4 | ЁЁ ЁЁ | Ё |
(2)ЩшдкМзИДгЁЕъИДгЁЪеЗбy1дЊЃЌдкввИДгЁЕъИДгЁЪеЗбy2дЊЃЌЗжБ№аДГіy1ЃЌy2ЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
(3)ЕБxЃО70ЪБЃЌЙЫПЭдкФФМвИДгЁЕъИДгЁЛЈЗбЩйЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋЁїABCбиBCЗНЯђЦНвЦ2cmЕУЕНЁїDEFЃЌШєЁїABCЕФжмГЄЮЊ16cmЃЌtЫФоxаЮABFDЕФжмГЄЮЊ( )

A. 16cmB. 18cmC. 20cmD. 22cm
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ФквЛЕуЃЌСЌНг
ФквЛЕуЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
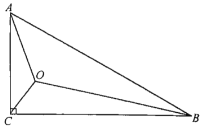
ЃЈ1ЃЉвдЕу![]() ЮЊа§зЊжааФЃЌНЋ
ЮЊа§зЊжааФЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыЗНЯђа§зЊ60ЁуЃЌЕУЕН
ЫГЪБеыЗНЯђа§зЊ60ЁуЃЌЕУЕН![]() ЃЈЕУЕН
ЃЈЕУЕН![]() ЁЂ
ЁЂ![]() ЕФЖдгІЕуЗжБ№ЮЊЕу
ЕФЖдгІЕуЗжБ№ЮЊЕу![]() ЁЂ
ЁЂ![]() ЃЉЃЌАДвЊЧѓЛЭМЃЈБЃСєзїЭМКлМЃЃЉЃЎ
ЃЉЃЌАДвЊЧѓЛЭМЃЈБЃСєзїЭМКлМЃЃЉЃЎ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЧѓ![]() ЕФЖШЪ§МА
ЕФЖШЪ§МА![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
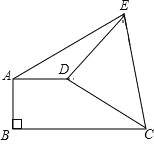
ЁОЬтФПЁПШчЭМЃЌADЁЮBCЃЌABЁЭBCгкЕуBЃЌAD=4ЃЌНЋCDШЦЕуDФцЪБеыа§зЊ90ЁужСDEЃЌСЌНгAEЁЂCEЃЌШєЁїADEЕФУцЛ§ЮЊ6ЃЌдђBC=_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧФГНЬЪвРяШеЙтЕЦЕФЫФИіПижЦПЊЙиЃЈЗжБ№МЧЮЊAЁЂBЁЂCЁЂDЃЉЃЌУПИіПЊЙиЗжБ№ПижЦвЛХХШеЙтЕЦЃЈПЊЙиађКХгыШеЙтЕЦЕФХХЪ§ађКХВЛвЛЖЈвЛжТЃЉЃЎФГЬьЩЯПЮЪБЃЌЭѕРЯЪІдкЭъШЋВЛжЊЕРФФИіПЊЙиЖдгІПижЦФФХХШеЙтЕЦЕФЧщПіЯТЯШКѓЫцЛњАДЯТСНИіПЊЙиЃЎ
ЃЈ1ЃЉЧѓЭѕРЯЪІАДЯТЕквЛИіПЊЙиЧЁКУФмДђПЊЕквЛХХШеЙтЕЦЕФИХТЪЃЛ
ЃЈ2ЃЉЭѕРЯЪІАДЯТСНИіПЊЙиЧЁКУФмДђПЊЕквЛХХгыЕкШ§ХХШеЙтЕЦЕФИХТЪЪЧЖрЩйЃПЧыСаБэИёЛђЛЪїзДЭММгвдЗжЮіЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com