
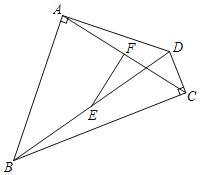
【题目】如图,四边形ABCD中,∠BAD=90°,∠DCB=90°,E、F分别是BD、AC的中点.
(1)请你猜想EF与AC的位置关系,并给予证明;
(2)当AC=16,BD=20时,求EF的长.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
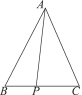
【题目】如图,△ABC中,AB=AC,∠BAC=50°,P是BC边上一点,将△ABP绕点A逆时针旋转50°,点P旋转后的对应点为点P′.
(1)画出旋转后的三角形;
(2)连接PP′,若∠BAP=20°,求∠PP′C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
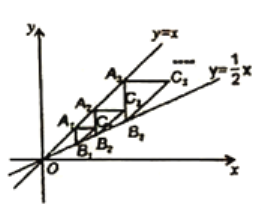
【题目】如图,点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,以点
,以点![]() 为直角顶点,
为直角顶点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,再过点
,再过点![]() 作
作![]() 轴,分别交直线
轴,分别交直线![]() 和
和![]() 于
于![]() ,
,![]() 两点,以点
两点,以点![]() 为直角顶点,
为直角顶点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() 按此规律进行下去,则等腰直角
按此规律进行下去,则等腰直角![]() 的面积为_______,等腰直角
的面积为_______,等腰直角![]() 的面积为______.
的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一元二次方程中,两实根之和为1的是 ( )
A. x2—x+1=0 B. x2+x—3=0 C. 2 x2-x-1=0 D. x2-x-5=0
查看答案和解析>>
科目:初中数学 来源: 题型:
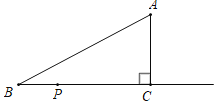
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=7.5cm,AC=4.5cm,动点P从点B出发沿射线BC以2cm/s的速度移动,设运动的时间为t秒,当△ABP为等腰三角形时,t的取值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() ,经过A、B的直线
,经过A、B的直线![]() 以每秒1个单位的
以每秒1个单位的
速度向下作匀速平移运动,与此同时,点P从点B出发,在直线![]() 上以每秒1个单位的速度沿直线
上以每秒1个单位的速度沿直线![]() 向右下方向作匀速运动.设它们运动的时间为
向右下方向作匀速运动.设它们运动的时间为![]() 秒.
秒.

(1)用含![]() 的代数式表示点P的坐标;
的代数式表示点P的坐标;
(2)过O作OC⊥AB于C,过C作CD⊥![]() 轴于D,问:
轴于D,问: ![]() 为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时
为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时![]() 与直线CD的位置关系.
与直线CD的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
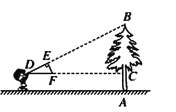
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古语说:“春眠不觉晓”,每到初春时分,想必有不少人变得嗜睡,而且睡醒后精神不佳.我们可以在饮食方面进行防治,比如以下食物可防治春困:香椿、大蒜、韭菜、山药、麦片.春天即将来临时,某商人抓住商机,购进甲、乙、丙三种麦片,已知销售每袋甲种麦片的利润率为10%,每袋乙种麦片的利润率为20%,每袋丙种麦片的利润率为30%,当售出的甲、乙、丙三种麦片的袋数之比为1:3:1时,商人得到的总利润率为22%;当售出的甲、乙、丙三种变片的袋数之比为3:2:1时,商人得到的总利润率为20%:那么当售出的甲、乙、丙三种麦片的袋数之比为2:3;4时,这个商人得到的总利润率为_____(用百分号表最终结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
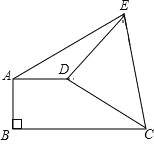
【题目】如图,AD∥BC,AB⊥BC于点B,AD=4,将CD绕点D逆时针旋转90°至DE,连接AE、CE,若△ADE的面积为6,则BC=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com