
【题目】(1)如图(a)所示,点![]() 是正方形
是正方形![]() 内的一点,把
内的一点,把![]() 绕点
绕点![]() 顺时针方向旋转,使点
顺时针方向旋转,使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点是
的对应点是![]() .若
.若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
(2)如图(b)所示,点![]() 是等边三角形
是等边三角形![]() 内的一点,若
内的一点,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
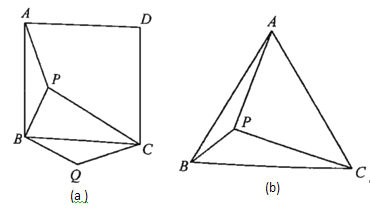
【答案】(1)135°;(2)150°
【解析】
(1)根据题意得出△ABP绕点B顺时针方向旋转了90°,才使点A与C重合,进而得出∠PBQ=90°,再利用勾股定理逆定理得出∠PQC的度数,进而求出∠BQC的度数;
(2)由题意可得出:△ABP绕点B顺时针方向旋转60°,才使点A与C重合,进而得出∠PP'C=90°,即可得出∠BPA的度数.
(1)如图(a)所示,连接![]() .
.
由旋转可知:![]() ,
,![]() .
.
又∵四边形![]() 是正方形,
是正方形,
∴![]() 绕点
绕点![]() 顺时针方向旋转了90°,才使点
顺时针方向旋转了90°,才使点![]() 与
与![]() 重合.
重合.
即![]() ,
,
∴![]() 是等腰直角三角形.
是等腰直角三角形.
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
故![]() .
.
(2)如图(b)所示,作![]() ,且
,且![]() ,连接
,连接![]() ,
,
∴![]() 是等边三角形.∴
是等边三角形.∴![]() ,
,![]() .
.
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
∴∠ABP+∠PBC=∠PBC+∠CBP',
∴![]() .∴
.∴![]() .
.
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
故![]() .
.



科目:初中数学 来源: 题型:
【题目】下列一元二次方程中,两实根之和为1的是 ( )
A. x2—x+1=0 B. x2+x—3=0 C. 2 x2-x-1=0 D. x2-x-5=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古语说:“春眠不觉晓”,每到初春时分,想必有不少人变得嗜睡,而且睡醒后精神不佳.我们可以在饮食方面进行防治,比如以下食物可防治春困:香椿、大蒜、韭菜、山药、麦片.春天即将来临时,某商人抓住商机,购进甲、乙、丙三种麦片,已知销售每袋甲种麦片的利润率为10%,每袋乙种麦片的利润率为20%,每袋丙种麦片的利润率为30%,当售出的甲、乙、丙三种麦片的袋数之比为1:3:1时,商人得到的总利润率为22%;当售出的甲、乙、丙三种变片的袋数之比为3:2:1时,商人得到的总利润率为20%:那么当售出的甲、乙、丙三种麦片的袋数之比为2:3;4时,这个商人得到的总利润率为_____(用百分号表最终结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,則四辺形ABFD的周长为( )

A. 16cmB. 18cmC. 20cmD. 22cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 内一点,连接
内一点,连接![]() 、
、![]() 、
、![]() ,且
,且![]() .
.
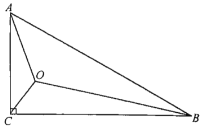
(1)以点![]() 为旋转中心,将
为旋转中心,将![]() 绕点
绕点![]() 顺时针方向旋转60°,得到
顺时针方向旋转60°,得到![]() (得到
(得到![]() 、
、![]() 的对应点分别为点
的对应点分别为点![]() 、
、![]() ),按要求画图(保留作图痕迹).
),按要求画图(保留作图痕迹).
(2)在(1)的条件下,求![]() 的度数及
的度数及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏的爸爸买了某项体育比赛的一张门票,她和哥哥两人都很想去观看.可门票只有一张,读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2,3,5,9的四张牌给小敏,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将两人抽出的两张扑克牌数字相加,如果和为偶数,则小敏去;如果和为奇数,则哥哥去.
【1】请用画树形图或列表的方法求小敏去看比赛的概率;
【2】哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
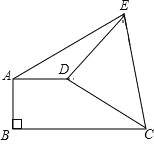
【题目】如图,AD∥BC,AB⊥BC于点B,AD=4,将CD绕点D逆时针旋转90°至DE,连接AE、CE,若△ADE的面积为6,则BC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=![]() =
=![]() ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】附加题:
探究题:我们知道等腰三角形的两个底角相等,如下面每个图中的△ABC中AB、BC是两腰,所以∠BAC=∠BCA.利用这条性质,解决下面的问题:
已知下面的正多边形中,相邻四个顶点连接的对角线交于点O它们所夹的锐角为a.如图:

正五边形α=_____;正六边形α=______;正八边α=_____;当正多边形的边数是n时,α=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com