
【题目】附加题:
探究题:我们知道等腰三角形的两个底角相等,如下面每个图中的△ABC中AB、BC是两腰,所以∠BAC=∠BCA.利用这条性质,解决下面的问题:
已知下面的正多边形中,相邻四个顶点连接的对角线交于点O它们所夹的锐角为a.如图:

正五边形α=_____;正六边形α=______;正八边α=_____;当正多边形的边数是n时,α=______.
【答案】α5=172°;α6=60°,α8=45°,α=![]() .
.
【解析】
如图,延长BA到F,根据多边形外角和为360°可得∠EAF的度数,根据正多边形内角和可得∠ABC=∠BAE=108°,利用等腰三角形的性质可得∠BAC=∠BCA=∠ABE=∠BEA=36°,利用三角形外角性质可得α=∠EAF,即可得正五边形中α的值,讨论可得α6、α8的值,根据所得规律即可得当正多边形的边数是n时α的值.
如图,延长BA到F,
∵∠EAF是正五边形ABCDE的外角,
∴∠EAF=360°÷5=72°,
∵五边形ABCDE是正五边形,
∴AB=BC=AE,∠ABC=∠BAE=(5-2)×180°÷5=108°,
∴∠BAC=∠BCA=∠ABE=∠BEA=![]() =36°,
=36°,
∵α=∠ABE+∠BAC,∠EAF=∠ABE+∠AEB,
∴α=∠EAF=72°,
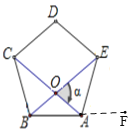
同理:α6=360°÷6=60°,α8=360°÷8=45°,
当正多边形的边数是n时,α=![]() .
.
故答案为36°;60°;45°;![]()


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
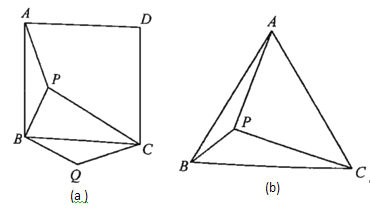
【题目】(1)如图(a)所示,点![]() 是正方形
是正方形![]() 内的一点,把
内的一点,把![]() 绕点
绕点![]() 顺时针方向旋转,使点
顺时针方向旋转,使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点是
的对应点是![]() .若
.若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
(2)如图(b)所示,点![]() 是等边三角形
是等边三角形![]() 内的一点,若
内的一点,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育行政部门为了了解八年级学生每学期参加综合实践活动的情况,随机抽样调查了该县八年级学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).
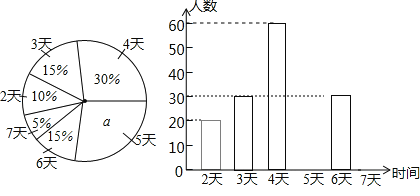
请你根据图中提供的信息,回答下列问题:
(1)求出参加抽样调查的八年级学生人数,并将频数直方图补充完整.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该县共有八年级学生![]() 人,请你估计“活动时间不少于
人,请你估计“活动时间不少于![]() 天”的大约有多少人?
天”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() 为
为![]() 边所在直线上的动点(不与点
边所在直线上的动点(不与点![]() 、
、![]() 重合),连结
重合),连结![]() ,以
,以![]() 为边作
为边作![]() ,且
,且![]() ,根据
,根据![]() ,得到
,得到![]() ,结合
,结合![]() ,
,![]() 得出
得出![]() ,发现线段
,发现线段![]() 与
与![]() 的数量关系为
的数量关系为![]() ,位置关系为
,位置关系为![]() ;
;
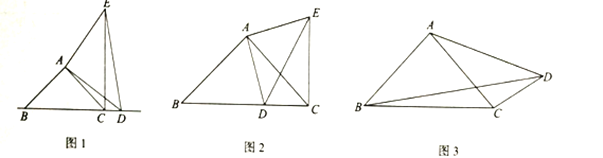
(1)探究证明:如图![]() ,在
,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,且点
,且点![]() 在
在![]() 边上滑动(点
边上滑动(点![]() 不与点
不与点![]() 、
、![]() 重合),连接
重合),连接![]() .
.
①则线段![]() ,
,![]() ,
,![]() 之间满足的等量关系式为_____;
之间满足的等量关系式为_____;
②求证: ![]() ;
;
(2)拓展延伸:如图![]() ,在四边形
,在四边形![]() 中,
中,![]() .若
.若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
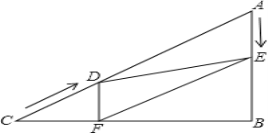
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个动点到达终点时,另一个动点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)当t为何值时,DF=DA?
(2)当t为何值时,△ADE为直角三角形?请说明理由.
(3)是否存在某一时刻t,使点F在线段AC的中垂线上,若存在,请求出t值,若不存在,请说明理由.
(4)请用含有t式子表示△DEF的面积,并判断是否存在某一时刻t,使△DEF的面积是△ABC面积的![]() ,若存在,请求出t值,若不存在,请说明理由.
,若存在,请求出t值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
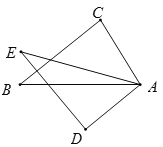
【题目】如图,已知,![]() ,AC=AD.给出下列条件: ①AB=AE;②BC=ED;③
,AC=AD.给出下列条件: ①AB=AE;②BC=ED;③![]() ;④
;④ ![]() .其中能使
.其中能使![]() 的条件为__________ (注:把你认为正确的答案序号都填上).
的条件为__________ (注:把你认为正确的答案序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,他们将全部测试成绩分成![]() 、
、![]() 、
、![]() 、
、![]() 四组,绘制了如下统计图表:
四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计图表
组别 | 分数/分 | 频数 | 各组总分/分 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
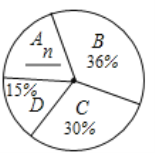
依据以上统计信息,解答下列问题:
(1)求得![]() _____,
_____,![]() ______;
______;
(2)这次测试成绩的中位数落在______组;
(3)求本次全部测试成绩的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上依次有A,C,B三地,甲、乙两人同时出发,甲从A地骑自行车去B地,途经C地休息1分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行从B地前往A地.甲、乙两人距A地的路程y(米)与时间x(分)之间的函数关系如图所示,请结合图象解答下列问题:
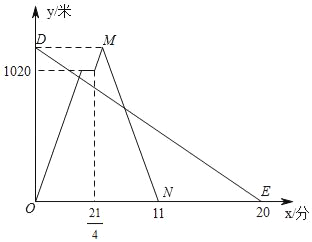
(1)请写出甲的骑行速度为 米/分,点M的坐标为 ;
(2)求甲返回时距A地的路程y与时间x之间的函数关系式(不需要写出自变量的取值范围);
(3)请直接写出两人出发后,在甲返回A地之前,经过多长时间两人距C地的路程相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com