
【题目】如图,已知抛物线与x轴交于A(﹣1,0),B(4,0),与y轴交于C(0,﹣2).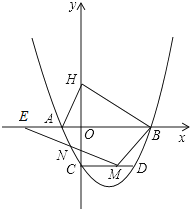
(1)求抛物线的解析式;
(2)H是C关于x轴的对称点,P是抛物线上的一点,当△PBH与△AOC相似时,求符合条件的P点的坐标(求出两点即可);
(3)过点C作CD∥AB,CD交抛物线于点D,点M是线段CD上的一动点,作直线MN与线段AC交于点N,与x轴交于点E,且∠BME=∠BDC,当CN的值最大时,求点E的坐标.
【答案】
(1)
解:∵抛物线与x轴交于A(﹣1,0),B(4,0),
∴设抛物线的解析式为:y=a(x+1)(x﹣4),
把(0,﹣2)代入y=a(x+1)(x﹣4),
∴a= ![]() ,
,
∴抛物线的解析式为:y= ![]() x2﹣
x2﹣ ![]() x﹣2
x﹣2
(2)
解:当△PBH与△AOC相似时,
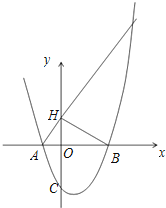
∴△AOC是直角三角形,
∴△PBH也是直角三角形,
由题意知:H(0,2),
∴OH=2,
∵A(﹣1,0),B(4,0),
∴OA=1,OB=4,
∴ ![]()
∵∠AOH=∠BOH,
∴△AOH∽△BOH,
∴∠AHO=∠HBO,
∴∠AHO+∠BHO=∠HBO+∠BHO=90°,
∴∠AHB=90°,
设直线AH的解析式为:y=kx+b,
把A(﹣1,0)和H(0,2)代入y=kx+b,
∴ ![]() ,
,
∴解得 ![]() ,
,
∴直线AH的解析式为:y=2x+2,
联立 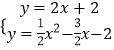 ,
,
解得:x=1或x=﹣8,
当x=﹣1时,
y=0,
当x=8时,
y=18
∴P的坐标为(﹣1,0)或(8,18)
(3)
解:过点M作MF⊥x轴于点F,
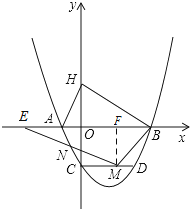
设点E的坐标为(n,0),M的坐标为(m,0),
∵∠BME=∠BDC,
∴∠EMC+∠BME=∠BDC+∠MBD,
∴∠EMC=∠MBD,
∵CD∥x轴,
∴D的纵坐标为﹣2,
令y=﹣2代入y= ![]() x2﹣
x2﹣ ![]() x﹣2,
x﹣2,
∴x=0或x=3,
∴D(3,﹣2),
∵B(4,0),
∴由勾股定理可求得:BD= ![]() ,
,
∵M(m,0),
∴MD=3﹣m,CM=m(0≤m≤3)
∴由抛物线的对称性可知:∠NCM=∠BDC,
∴△NCM∽△MDB,
∴ ![]() ,
,
∴ ![]() ,
,
∴CN= ![]() =﹣
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当m= ![]() 时,CN可取得最大值,
时,CN可取得最大值,
∴此时M的坐标为( ![]() ,﹣2),
,﹣2),
∴MF=2,BF= ![]() ,MD=
,MD= ![]()
∴由勾股定理可求得:MB= ![]() ,
,
∵E(n,0),
∴EB=4﹣n,
∵CD∥x轴,
∴∠NMC=∠BEM,∠EBM=∠BMD,
∴△EMB∽△BDM,
∴ ![]() ,
,
∴MB2=MDEB,
∴ ![]() =
= ![]() ×(4﹣n),
×(4﹣n),
∴n=﹣ ![]() ,
,
∴E的坐标为(﹣ ![]() ,0).
,0).
【解析】(1)设抛物线的解析式为y=a(x+1)(x﹣4),然后将(0,﹣2)代入解析式即可求出a的值;(2)当△PBH与△AOC相似时,△PBH是直角三角形,由 ![]() 可知∠AHB=90°,所以求出直线AH的解析式后,联立一次函数与二次函数的解析式后即可求出P的坐标;(3)设M的坐标为(m,0),由∠BME=∠BDC可知∠EMC=∠MBD,所以△NCM∽△MDB,利用对应边的比相等即可得出CN与m的函数关系式,利用二次函数的性质即可求出m=
可知∠AHB=90°,所以求出直线AH的解析式后,联立一次函数与二次函数的解析式后即可求出P的坐标;(3)设M的坐标为(m,0),由∠BME=∠BDC可知∠EMC=∠MBD,所以△NCM∽△MDB,利用对应边的比相等即可得出CN与m的函数关系式,利用二次函数的性质即可求出m= ![]() 时,CN有最大值,然后再证明△EMB∽△BDM,即可求出E的坐标.本题考查函数的综合问题,涉及待定系数法求解析式,联立解析式求交点坐标,相似三角形判定与性质,二次函数最值等知识,内容较为综合,需要学生灵活运用知识去解决问题.
时,CN有最大值,然后再证明△EMB∽△BDM,即可求出E的坐标.本题考查函数的综合问题,涉及待定系数法求解析式,联立解析式求交点坐标,相似三角形判定与性质,二次函数最值等知识,内容较为综合,需要学生灵活运用知识去解决问题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
【题目】我们根据指数运算,得出了一种新的运算,如表是两种运算对应关系的一组实例:
指数运算 | 21=2 | 22=4 | 23=8 | … | 31=3 | 32=9 | 33=27 | … |
新运算 | log22=1 | log24=2 | log28=3 | … | log33=1 | log39=2 | log327=3 | … |
根据上表规律,某同学写出了三个式子:①log216=4,②log525=5,③log2 ![]() =﹣1.其中正确的是( )
=﹣1.其中正确的是( )
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.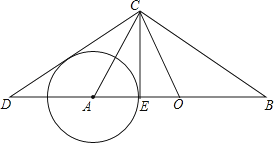
(1)求证:∠B=∠ACD.
(2)已知点E在AB上,且BC2=ABBE.
(i)若tan∠ACD= ![]() ,BC=10,求CE的长;
,BC=10,求CE的长;
(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与坐标轴分别交于A(﹣2,0),B(0,1)两点,与反比例函数的图象在第一象限交于点C(4,n),求一次函数和反比例函数的解析式.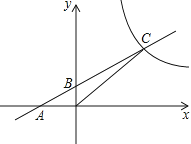
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.

解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线![]() :y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
:y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( ) 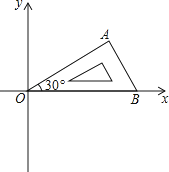
A.( ![]() ,﹣1)
,﹣1)
B.(1,﹣ ![]() )
)
C.( ![]() ,﹣
,﹣ ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年体育中考中,某班一学习小组6名学生的体育成绩如下表,则这组学生的体育成绩的众数,中位数,方差依次为( )
成绩(分) | 27 | 28 | 30 |
人数 | 2 | 3 | 1 |
A.28,28,1
B.28,27.5,1
C.3,2.5,5
D.3,2,5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批肥料,为了验证这批肥料的重量,抽出 10 袋进行称重,每袋以 50 千克为标准,超出部分记为正,不足部分记为负,10 袋的重量分别如下:+5,﹣3,﹣8,+6,+4,+8,﹣2,﹣12,+8,+5
(1)按每袋 50 千克为标准,抽出的 10 袋肥料的重量超出或不足多少千克?
(2)若购进这批肥料共有 500 袋,问这批肥料的总重量约为多少?
(3)若按每袋 120 元购进,140 元卖出,则卖完这批肥料的总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com