
【题目】已知:AB是⊙O的直径,DA、DC分别是⊙O的切线,点A、C是切点,连接DO交弧AC于点E,连接AE、CE.
(1)如图1,求证:EA=EC;
(2)如图2,延长DO交⊙O于点F,连接CF、BE交于点G,求证:∠CGE=2∠F;
(3)如图3,在(2)的条件下,DE=![]() AD,EF=2
AD,EF=2![]() , 求线段CG的长.
, 求线段CG的长.
【答案】证明:(1)如图1,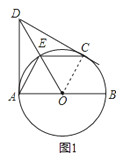
连接OC,
∵DA、DC分别是⊙O的切线,点A、C是切点,OA、OC是半径,
∴OA⊥DA,OC⊥DC,
∴∠DAO=∠DCO=90°,
在Rt△ODA和Rt△ODC中,![]() ,
,
∴Rt△ODA≌Rt△ODC,
∴∠EOA=∠EOC,
∴AE=CE;
(2)证明:如图2,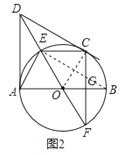
连接OC,BE,由(1)证得∠AOE=∠COE,
又∵∠B=![]() ∠AOE,∠F=
∠AOE,∠F=![]() ∠COE,
∠COE,
∴∠B=∠F,
∵OB=OE,
∴∠B=∠OEB,
∴∠F=∠OEG,
∵∠EGC是△EGF的外角,
∴∠EGC=∠F+∠GEF=2∠F,
即∠EGC=2∠F;
(3)解:∵EF是⊙O的直径,
∴∠ECF=90°
∵EF=2![]() ,
,
∴OA=OE=![]() EF=
EF=![]() ,
,
∵DE=![]() AD,设DE=m,
AD,设DE=m,
∴AD=2m,
在Rt△DAO中,OA2+DA2=OD2 ,
∴![]() ,
,
解得m1=0(舍去),m2=![]() ,
,
∴DA=![]()
![]() ,DO=
,DO=![]()
![]() ,
,
∴在Rt△ADO中,tan∠DOA=![]() =
=![]() ,cos∠DOA=
,cos∠DOA=![]() =
=![]() ,
,
∵∠EOA=2∠B,∠EGC=2∠F,
∴∠EGC=∠EOA,
∴tan∠EGC=![]() ,
,
如图3,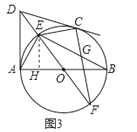
过点E作EH⊥AB于点H,
在Rt△EOH中OH=OEcos∠EOH=![]() X
X![]() =
=![]()
![]() ,
,
∴EH=![]()
![]() AH=AO﹣OH=
AH=AO﹣OH=![]() -
-![]()
![]() =
=![]()
![]() ,
,
在Rt△EHA中,EA2=AH2+EH2 ,
∴EA=2,
∵AE=CE,
∴EC=2,
在Rt△ECG中,tan∠EGC=![]() =
=![]() =
=![]() ,
,
∴GC=![]() .
.
【解析】(1)连接OC,根据切线的性质得到OA⊥DA,OC⊥DC,由垂直的定义得到∠DAO=∠DCO=90°,推出Rt△ODA≌Rt△ODC,根据全等三角形的性质得到∠EOA=∠EOC,由等腰三角形的判定得到结论;
(2)连接OC,BE,由(1)证得∠AOE=∠COE,根据圆周角定理得到∠B=![]() ∠AOE,∠F=
∠AOE,∠F=![]() ∠COE,得到∠B=∠F,根据等腰三角形的性质得到∠B=∠OEB,于是得到∠F=∠OEG,根据三角形的外角的性质即可得到结论;
∠COE,得到∠B=∠F,根据等腰三角形的性质得到∠B=∠OEB,于是得到∠F=∠OEG,根据三角形的外角的性质即可得到结论;
(3)由圆周角定理得到∠ECF=90°求得OA=OE=![]() EF=
EF=![]() , 设DE=m,AD=2m,根据勾股定理列方程得到m1=0(舍去),m2=
, 设DE=m,AD=2m,根据勾股定理列方程得到m1=0(舍去),m2=![]() , 于是得到DA=DA=
, 于是得到DA=DA=![]()
![]() , DO=
, DO=![]()
![]() , 在Rt△ADO中,tan∠DOA=
, 在Rt△ADO中,tan∠DOA=![]() =
=![]() , cos∠DOA=
, cos∠DOA=![]() =
=![]() , 得到tan∠EGC=
, 得到tan∠EGC=![]() , 过点E作EH⊥AB于点H,在Rt△EOH中OH=OEcos∠EOH=
, 过点E作EH⊥AB于点H,在Rt△EOH中OH=OEcos∠EOH=![]() X
X![]() =
=![]()
![]() , 于是得到EH=
, 于是得到EH=![]()
![]() AH=AO﹣OH=
AH=AO﹣OH=![]() -
-![]()
![]() =
=![]()
![]() , 根据勾股定理求得EC=2,根据三角函数的定义即可得到结论.
, 根据勾股定理求得EC=2,根据三角函数的定义即可得到结论.


科目:初中数学 来源: 题型:
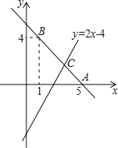
【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.
(1)求证:ABAF=CBCD;
(2)已知AB=15cm,BC=9cm,P是线段DE上的动点.设DP=x cm,梯形BCDP的面积为ycm2 .
①求y关于x的函数关系式.
②y是否存在最大值?若有求出这个最大值,若不存在请说明理由.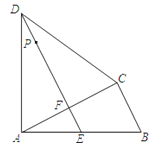
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形;②△HED的面积是1﹣![]() ;③∠AFG=112.5°;④BC+FG=
;③∠AFG=112.5°;④BC+FG=![]() .其中正确的结论是( )
.其中正确的结论是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
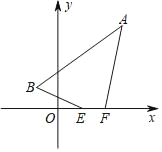
【题目】已知点A(3,4),点B(﹣1,1),在x轴上有两动点E、F,且EF=1,线段EF在x轴上平移,当四边形ABEF的周长取得最小值时,点E的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
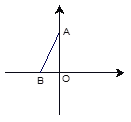
【题目】如图,在平面直角坐标系中,点A,B分别在y轴和x轴上,∠ABO=60°,在坐标轴上找一点P,使得△PAB是等腰三角形,则符合条件的点P共有( )
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知C为线段AB的中点,E为线段AB上的点,点D为线段AE的中点.
(1)若线段AB=a,CE=b,|a﹣15|+(b﹣4.5)2=0,求a,b的值;
(2)如图1,在(1)的条件下,求线段DE的长;
(3)如图2,若AB=15,AD=2BE,求线段CE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”【注释】1步=5尺.
译文:“当秋千静止时,秋千上的踏板离地有1尺高,如将秋千的踏板往前推动两步(10尺)时,踏板就和人一样高,已知这个人身高是5尺.美丽的姑娘和才子们,每天都来争荡秋千,欢声笑语终日不断.好奇的能工巧匠,能算出这秋千的绳索长是多少吗?”
如图,假设秋千的绳索长始终保持直线状态,OA是秋千的静止状态,A是踏板,CD是地面,点B是推动两步后踏板的位置,弧AB是踏板移动的轨迹.已知AC=1尺,CD=EB=10尺,人的身高BD=5尺.设绳索长OA=OB=x尺,则可列方程为 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com