练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
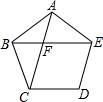
    11．如图，在正五边形ABCDE中，对角线AC、BE相交于点F，则F为线段BE的黄金分割点，若EF=2，则BE=$\sqrt{5}$+1．

    分析 根据黄金比为$\frac{\sqrt{5}-1}{2}$进行计算即可得到答案．

    解答 解：∵F为线段BE的黄金分割点，EF＞BE，
    ∴EF=$\frac{\sqrt{5}-1}{2}$BE，又EF=2，
    ∴BE=$\sqrt{5}$+1，
    故答案为：$\sqrt{5}$+1．

    点评 本题考查的是黄金分割的知识，把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．下列调查中，适宜采用全面调查方式的是（　　）
    A．旅客上飞机前的安全检查
    B．对广州市七年级学生身高现状的调查
    C．多某品牌食品安全的调查
    D．对一批灯管使用寿命的调查

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算
    （1）计算：$\root{3}{8}$+$\sqrt{（-2）^{2}}$-$\sqrt{\frac{1}{4}}$       
    （2）解方程组：$\left\{\begin{array}{l}{x-2y=4}\\{5x-y=11}\end{array}\right.$
    （3）解不等式组$\left\{\begin{array}{l}{x+2≥1}\\{2（x+3）-3＞3x}\end{array}\right.$，并将解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列图案中，既是轴对称图形又是中心对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

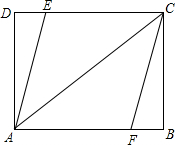    6．如图，矩形ABCD中，AB=8，AD=6，点E、F分别在边CD、AB上．
    （1）若DE=BF，求证：四边形AFCE是平行四边形；
    （2）若四边形AFCE是菱形，求菱形AFCE的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．如图所示的几何体的俯视图是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知二次函数y=x2+m（2x+1）+1，当x=1时，y=-1，将其化为y=ax2+bx+c的形式，并求出其中a，b，c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．用夹逼法估计一下$\sqrt{9000}$的值，精确到0.1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

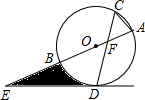    1．如图，⊙O的直径AB与弦CD相交于点F，且∠ACD=60°，在AB的延长线上取一点E，使得∠AED=30°．
    （1）求证：直线DE与⊙O相切于点D；
    （2）若图中DE=$\sqrt{3}$，求图中阴影部分图形的面积（结果保留3个有效数字）（备用数据：$\sqrt{3}$≈1.732，π≈3.142）

    查看答案和解析>>

    同步练习册答案