
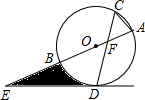
 如图,⊙O的直径AB与弦CD相交于点F,且∠ACD=60°,在AB的延长线上取一点E,使得∠AED=30°.
如图,⊙O的直径AB与弦CD相交于点F,且∠ACD=60°,在AB的延长线上取一点E,使得∠AED=30°.分析 (1)连接OD,根据圆周角定理求得∠AOD=120°,从而求得∠EOD=60°,根据三角形内角和定理求得∠ODE=90°,即可证得结论;
(2)解直角三角形求得半径OD,然后根据S阴影=S△ODE-S扇形求得即可.
解答 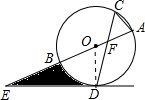 (1)证明:连接OD,
(1)证明:连接OD,
∵∠ACD=60°,
∴∠AOD=120°,
∴∠EOD=60°,
∵∠AED=30°,
∴∠ODE=90°,
∴直线DE与⊙O相切于点D;
(2)解:在RT△ODE中,∠AED=30°,DE=$\sqrt{3}$,
∴OD=tag30°•ED=$\frac{\sqrt{3}}{3}$×$\sqrt{3}$=1,
∴S△ODE=$\frac{1}{2}$ED•OD=$\frac{1}{2}$×$\sqrt{3}×1$=$\frac{\sqrt{3}}{2}$,
∵∠BOD=60°,OD=1,
∴S扇形=$\frac{60×π×{1}^{2}}{360}$=$\frac{π}{6}$,
∴S阴影=S△ODE-S扇形=$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$≈0.342.
点评 本题考查了切线的判定,解正切函数,扇形的面积等,作出辅助线构建直角三角形是解题的关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:填空题
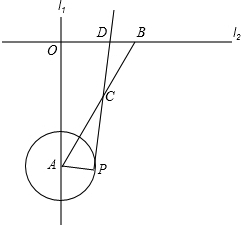 如图,直线l1⊥l2,垂足为O,点A、B分别在直线l1和l2上,∠OAB=30°,OB=2,以A为圆心,1为半径画圆,点P在圆A的圆周上运动,连接AP,过点P画PA的垂线与线段AB相交于点C,与直线l2相交于D,当AC=BC时,OD的长是1或4.
如图,直线l1⊥l2,垂足为O,点A、B分别在直线l1和l2上,∠OAB=30°,OB=2,以A为圆心,1为半径画圆,点P在圆A的圆周上运动,连接AP,过点P画PA的垂线与线段AB相交于点C,与直线l2相交于D,当AC=BC时,OD的长是1或4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
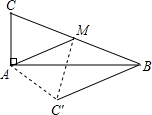 如图,在Rt△ABC中,∠BAC=90°,点M为斜边BC的中点,AM=5厘米,∠AMC=45°,将△AMC沿AM翻折,点C落在△ABC所在平面内的C′处,那么四边形BC′AC的面积为$\frac{25\sqrt{2}+25}{2}$平方厘米.
如图,在Rt△ABC中,∠BAC=90°,点M为斜边BC的中点,AM=5厘米,∠AMC=45°,将△AMC沿AM翻折,点C落在△ABC所在平面内的C′处,那么四边形BC′AC的面积为$\frac{25\sqrt{2}+25}{2}$平方厘米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
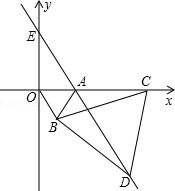 如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 明天某地区早晨有雾 | |
| B. | 抛掷一枚质地均匀的骰子,向上一面的点数是6 | |
| C. | 一个不透明的袋子中有2个红球和1个白球,从中摸出1个球,该球是黑球 | |
| D. | 明天见到的第一辆公交车的牌照的末位数字将是偶数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
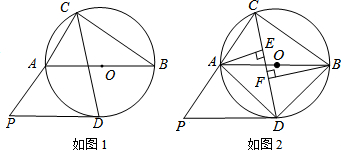
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
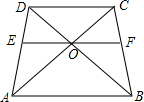 在梯形ABCD中,CD∥AB,AC、BD交于点O,过点O作AB的平行线交AD于点E,交BC于点F,则图中有5对相似形三角形;若DC=9,AB=15,则OD:OB=$\frac{3}{5}$,EF=$\frac{45}{4}$.
在梯形ABCD中,CD∥AB,AC、BD交于点O,过点O作AB的平行线交AD于点E,交BC于点F,则图中有5对相似形三角形;若DC=9,AB=15,则OD:OB=$\frac{3}{5}$,EF=$\frac{45}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com