Question

12．已知Rt△ABC中，∠C=90°，CH⊥AB于点H，AC=3，CH=2，求BC的长．

Answer 1

分析 根据勾股定理求得AB的长度，然后利用射影定理来求得BH、BC的长度．

解答 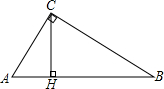解：∵Rt△ABC中，∠C=90°，CH⊥AB于点H，AC=3，CH=2，
∴AH²=AC²-CH²=5．
∴AH=$\sqrt{5}$．
又∵CH²=AH•BH，
∴BH=$\frac{4}{\sqrt{5}}$=$\frac{4\sqrt{5}}{5}$，
∴BC²=BH•AB=$\frac{4\sqrt{5}}{5}$×（$\sqrt{5}$+$\frac{4\sqrt{5}}{5}$）=$\frac{36}{5}$，则BC=$\frac{6\sqrt{5}}{5}$．

点评 本题考查了射影定理：
①直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项．
②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项．