
����Ŀ����֪������ABCD�У���ABC=60�㣬�Խ���AC��BD�ཻ�ڵ�O����E���߶�BD��һ���㣨�����B��D�غϣ�������AE����AEΪ����AE���Ҳ�������AEFG���ҡ�AEF=60�㣮
��1����ͼ1������F�����߶�BD�ϣ����жϣ��߶�EF���߶�DF��������ϵ��.
��2����ͼ2��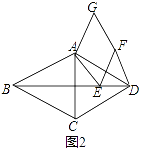
����F�����߶�BD�ϣ������������䣬��1���еĽ����Ƿ���Ȼ������������жϲ�����֤����
��3������C��E��G������ͬһֱ���ϣ������������䣬��ֱ��д���߶�BE���߶�BD����ϵ��
���𰸡�
��1��
�⣺��ͼ1������AF��

���ı���ABCD�����Σ�
��AC��BD����ABO= ![]() ��ABC=30�㣬
��ABC=30�㣬
���OAE=��OAF=30�㣬
���DAF=30��=��ADO��
��AF=FD��
��AF=EF��
��EF=FD��
�ߡ�AEF=60�㣬
���BAE=30��=��ABO��
��AE=BE
��2��
�⣺��������ͼ3��
����CE��AF��

���ı���ABCD�����Σ��ı���AEFG�����Σ�
��AD=CD��AE=EF��BD��ֱƽ��AC����ABC=��ADC=60�㣬
���ADC=��AEF=60�㣬
���ACD�͡�AEF�ǵȱ������Σ�
��AC=AD��AE=AF=EF����CAD=��EAF=60�㣬
���CAE=��DAF��
�ڡ�ACE�͡�ADF�У�  ��
��
��ACE�ա�ADF��
��EC=DF��
��BD��ֱƽ��AC��
��EC=AE��
��DF=AE=EF
��3��
�⣺��AE=CE��
���ACE=��CAE��
�ߵ�C��E��G��ͬһ��ֱ���ϣ�
���AEG=2��CAE=30�㣬
���CAE=15�㣬
�ߡ�BAO=60��㣬
���BAE=75�㣬
�ߡ�ABO= ![]() ��ABC=30�㣬
��ABC=30�㣬
���AEB=75��=��BAE��
��BE=AB��
��Rt��AOB�У���ABO=30�㣬
��cos��ABO= ![]() =
= ![]() ��
��
��OB= ![]() AB=
AB= ![]() BE��
BE��
��BD=2OB= ![]() BE
BE
����������1�����������ε����ʵó���ABO=��ADO=30�㣬AC��BD�����������FAD=30�㼴�ɵó����ۣ���2�����жϳ���ACD�͡�AEF�ǵȱ������Σ������ó���CAE=��DAF�������жϳ���ACE�ա�ADF�����ɵó����ۣ���3���������CAE=15�㣬�����жϳ�BE=AB�����ҳ�OB��AB�Ĺؼ����������ɵó����ۣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����һ��ƽ�Ƶ���DFE��λ�ã���ش��������⣺
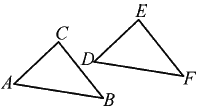
(1)��C�Ķ�Ӧ���ǵ�__________����D=__________��BC=__________��
(2)����CE����ôƽ�Ƶķ������__________�ķ���ƽ�Ƶľ�������߶�__________�ij��ȣ�
(3)����AD��BF��BE�����߶�CE��ȵ��߶���__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��E��BC���е㣬ACƽ�֡�BCD����AC��AB����DE����AC��F�� 
��1����֤��AD=CE��
��2������B=60�㣬��ȷ���ı���ABED��ʲô�����ı��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
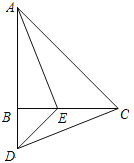
����Ŀ����ͼ������ABC�У�AB��CB����ABC��90�㣬DΪAB�ӳ�����һ�㣬��E��BC���ϣ���BE��BD������AE��DE��DC��
�� ��֤����ABE�ա�CBD��
�� ����CAE��30��������BDC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
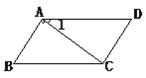
����Ŀ����ͼ����֪��1��30������B��60����AB��AC��
��1�����㣺��DAB����B
��2��AB��CDƽ����AD��BCƽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a>b��������>������<����գ�
(1)a��1________b��1��(2)![]() a________
a________![]() b��(3)a��c________b��c��(4)��3a________��3b��(5)��
b��(3)a��c________b��c��(4)��3a________��3b��(5)��![]() a��c________��
a��c________��![]() b��c.
b��c.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���֪�߶�AB=12cm����CΪ�߶�AB�ϵ�һ���㣬��D��E�ֱ���AC��BC�е�.
��1������Cǡ����AB���е㣬��DE=_______cm��
��2����AC=4cm����DE�ij���
��3����˵������ACȡ��ֵ��������12cm����DE�ij����䣻
��4����ͼ�ڣ���֪��AOB=120�㣬���ǵ��ڲ���һ��C������OC.��OD��OE�ֱ�ƽ�֡�AOC�͡�BOC.��˵����DOE�Ķ���������OC��λ����.
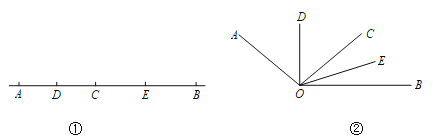
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͨ��ѧϰ�������֣������κ���y=ax2+bx+c��a��0����ͼ���㣨x1 �� y1������x2 �� y2����x1��x2������y1y2��0����ax2+bx+c=0��a��0����һ����x0��ȡֵ��Χ��x1��x0��x2 �� ������ȴ˷������ƶϷ���x3+x��1=0��ʵ����x0���ڷ�ΧΪ�� ��
A.�� ![]() ��x0��0
��x0��0
B.0��x0�� ![]()
C.![]() ��x0��1
��x0��1
D.1��x0�� ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com