
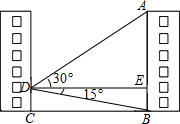
 如图,小明站在家中窗口选一个观测点D,测得正对面AB楼顶端A的仰角为30°,楼底B的俯角为15°,观测点D到楼AB的距离为27米.(结果用根号表示)
如图,小明站在家中窗口选一个观测点D,测得正对面AB楼顶端A的仰角为30°,楼底B的俯角为15°,观测点D到楼AB的距离为27米.(结果用根号表示)分析 (1)利用锐角三角函数关系得出cos∠ADE=$\frac{DE}{AD}$,进而求出AD的长;
(2)利用锐角三角函数关系表示出AB,BF的长,进而得出等式求出即可.
解答 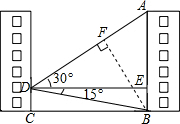 解:(1)在Rt△ADE中,
解:(1)在Rt△ADE中,
cos∠ADE=$\frac{DE}{AD}$,
AD=$\frac{DE}{cos∠ADE}$=$\frac{27}{cos30°}$=$\frac{27}{\frac{\sqrt{3}}{2}}$=18$\sqrt{3}$,
答:观测点D到楼顶A的距离是$18\sqrt{3}$米;
(2)作BF⊥AD,设AF=x,
∵∠BAD=90°-30°=60°,
∴∠ABF=30°,
∴AB=2x,
BF=$\sqrt{3}x$,∠BDF=45°,
∴DF=BF=$\sqrt{3}x$,
∴$\sqrt{3}x$+x=$18\sqrt{3}$,
$AB=2x=\frac{{36\sqrt{3}}}{{\sqrt{3}+1}}$=$54-18\sqrt{3}$),
答:楼AB的高度是(54-18$\sqrt{3}$)米.
点评 此题主要考查了解直角三角形,正确应用锐角三角函数关系是解题关键.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$ | B. | $\sqrt{7}$ | C. | $\root{2}{{\frac{1}{2}}}$ | D. | $\sqrt{20}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com