
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() 为
为![]() 的中点.
的中点.
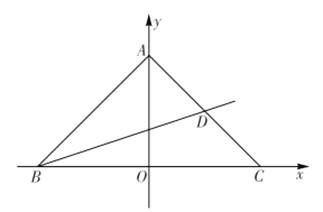
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 以每秒
以每秒![]() 个单位长度的速度运动,运动时间为
个单位长度的速度运动,运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() 求
求![]() 与
与![]() 的函数关系式,并直接写出自变量的取值范围;
的函数关系式,并直接写出自变量的取值范围;
(3)在(2)的条件下,是否存在点![]() 使
使![]() 是以
是以![]() 为腰的等腰三角形,若存在,直接写出点
为腰的等腰三角形,若存在,直接写出点![]() 的坐标;若不存在;请说明理由.
的坐标;若不存在;请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在
;(3)存在![]() ,
,![]() .
.
【解析】
(1)根据已知条件可得出点A、B的坐标,再根据![]() 得出点C的坐标,再利用待定系数法求直线AC解析式即可;
得出点C的坐标,再利用待定系数法求直线AC解析式即可;
(2)先求出点D的坐标为![]() ,利用勾股定理可得出
,利用勾股定理可得出![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,利用三角形的面积可得出AF的值,当运动时间为
,利用三角形的面积可得出AF的值,当运动时间为![]() 秒时,
秒时,![]() ,分点
,分点![]() 在线段
在线段![]() 上运动时,即
上运动时,即![]() 时和点
时和点![]() 在线段
在线段![]() 延长线上运动时,即
延长线上运动时,即![]() 时两种情况分析.
时两种情况分析.
(3)分![]() 和
和![]() 两种情况,当
两种情况,当![]() 时,
时,![]() ,但
,但![]() 不垂直
不垂直![]() ,此种情况不符合题意;当
,此种情况不符合题意;当![]() 时,可知点
时,可知点![]() 的纵坐标为
的纵坐标为![]() ,可得
,可得![]() ,解方程即可.
,解方程即可.
解:![]() 令
令![]() 中
中![]()
则![]() .
.
![]()
令![]() 中
中![]()
则![]()
![]()
![]() 点
点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]()
设直线![]() 的解析式为
的解析式为![]()
将点![]() 代入
代入![]() 中,
中,
得![]()
解得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
![]() 为
为![]() 的中点,
的中点,
![]() 点
点![]() 的坐标为
的坐标为![]()
![]() .
.
过点![]() 作
作![]() 交
交![]() 于点
于点![]() 如图,
如图,
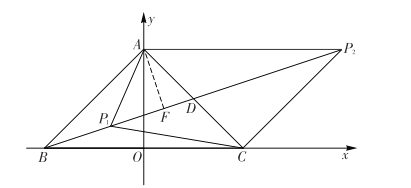
![]()
![]()
![]()
![]()
![]()
![]()
![]()
当点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 以每秒
以每秒![]() 个单位长度的速度运动,
个单位长度的速度运动,
运动时间为![]() 秒时,
秒时,![]()
当点![]() 在线段
在线段![]() 上运动时,即
上运动时,即![]() 时,
时,
![]()
![]()
![]() ;
;
当点![]() 在线段
在线段![]() 延长线上运动时,即
延长线上运动时,即![]() 时,
时,
![]()
![]()
![]()
综上所述:![]() 与
与![]() 的函数关系式为
的函数关系式为![]()
![]() 存在
存在![]() ,
,![]() .
.
如图,要使![]() 是等腰三角形,且以
是等腰三角形,且以![]() 为腰,有两种情况:
为腰,有两种情况:
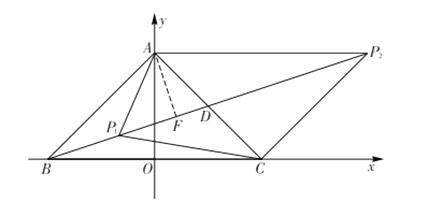
![]()
![]() 但
但![]() 不垂直
不垂直![]()
![]() 此种情况不存在;
此种情况不存在;
![]() ,由题意,可知点
,由题意,可知点![]() 的纵坐标为
的纵坐标为![]()
可得![]()
解得![]()
![]() ,
,![]()


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2经过点A(1,0),B(4,0),交y轴于点C;
(1)求抛物线的解析式(用一般式表示);
(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC=![]() S△ABD?若存在,请求出点D坐标;若不存在,请说明理由;
S△ABD?若存在,请求出点D坐标;若不存在,请说明理由;
(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.
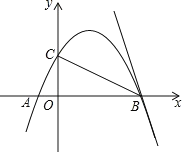
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的对称轴为x=﹣1,且过点(﹣3,0),(0,﹣3).
(1)求抛物线的表达式.
(2)已知点(m,k)和点(n,k)在此抛物线上,其中m≠n,请判断关于t的方程t2+mt+n=0是否有实数根,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx+b(k,b为常数,k≠0)与函数y=![]() 的图象交于点A(-1,m)
的图象交于点A(-1,m)
(1)求m;
(2)当k=______时,则直线l经过第一、三、四象限(任写一个符合题意的值即可);
(3)求(2)中的直线l的解析式和它与两坐标轴围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=3,点D在BC上且BD=2CD,E,F分别在AB,AC上运动且始终保持∠EDF=45°,设BE=x,CF=y,则y与x之间的函数关系用图象表示为:( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:
该产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com