
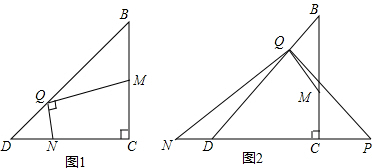
分析 (1)如图1,过Q点作QP⊥BD交DC于P,然后根据等腰直角三角形的性质的性质证明△QPN∽△QBM,就可以得出结论;
(2)根据余角的性质得到∠NQP=∠MQB,然后根据等腰直角三角形的性质的性质证明△QPN∽△QBM,就可以得出结论.
解答 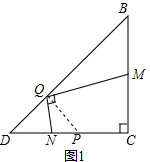 解:(1)如图1,过Q点作QP⊥BD交DC于P,
解:(1)如图1,过Q点作QP⊥BD交DC于P,
∴∠PQB=90°.
∵∠MQN=90°,
∴∠NQP=∠MQB,
∵CD=CB,∠BCD=90°,
∴∠DPQ=∠D=45°,DQ=PQ,
∴∠DPQ=∠DBC,
∴△QPN∽△QBM,
∴$\frac{QM}{QN}=\frac{BQ}{PQ}$,
∵BQ=3DQ,
∴BQ=3PQ,
∴$\frac{QM}{QN}$=$\frac{1}{3}$;
(2)∵QP⊥BD交DC于P,
∴∠PQD=90°.
∵∠MQN=90°,
∴∠NQP=∠MQB,
∵CD=CB,∠BCD=90°,
∴∠DPQ=∠D=45°,DQ=PQ,
∴∠DPQ=∠DBC,
∴△QPN∽△QBM,
∴$\frac{BM}{PN}$=$\frac{BQ}{PQ}$,
∵BQ=$\frac{1}{3}$DQ,
∴BQ=$\frac{1}{3}$PQ,
∴$\frac{BM}{PN}$=$\frac{1}{3}$.
点评 本题考查了相似三角形的判定与性质的运用,等腰直角三角形的性质,在解答时利用三角形相似的性质求出线段的比是解答本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
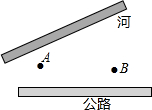 如图,公路与大河的中间地带有两个工厂A,B,现要在公路上建一仓库,在河边修一水泵站.
如图,公路与大河的中间地带有两个工厂A,B,现要在公路上建一仓库,在河边修一水泵站.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
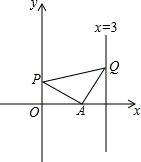 如图,在平面直角坐标系xOy中,点A的坐标为(2,0),Q是直线x=3上的一个动点,y轴正半轴上是否存在点P,使△APQ为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
如图,在平面直角坐标系xOy中,点A的坐标为(2,0),Q是直线x=3上的一个动点,y轴正半轴上是否存在点P,使△APQ为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com