
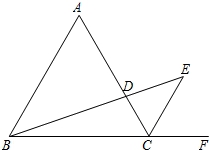
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长交CE于点E,若AB=6,AD=2CD,则BE的长为__________.
3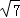 .
.
【考点】相似三角形的判定与性质;等边三角形的性质;勾股定理.
【分析】如图,作辅助线;证明AB∥CF,得到△ABD∽△CED,进而得到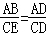 ,结合AD=2CD,AB=6,求出CE=3;求出EG、CG的长度,运用勾股定理即可解决问题.
,结合AD=2CD,AB=6,求出CE=3;求出EG、CG的长度,运用勾股定理即可解决问题.
【解答】解:如图,过点E作EG⊥CF于点G;
∵△ABC是 等边三角形,
等边三角形,
∴∠A=∠ACB=60°,AB=BC=6;
∴∠ACF=120°,而CE是外角平分线,
∴∠ACE=∠ECG=60°,∠A=∠ACE,
∴AB∥CF,△ABD∽△CED,
∴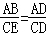 ,而AD=2CD,AB=6,
,而AD=2CD,AB=6,
∴CE=3;而∠ECG=60°,
∴∠CEG=30°,CG=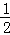 CE=1.5,EG=
CE=1.5,EG=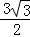 ,
,
∴BG=7.5;
由勾股定理得:BE2=BG2+EG2,
∴BE=3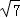 ,
,
故答案为3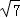 .
.

【点评】该题主要考查了等边三角形的性质、相似三角形的判定、勾股定理等几何知识点及其应用问题;解题的关键是作辅助线;灵活运用等边三角形的性质、相似三角形的判定、勾股定理等几何知识点来分析、判断、解答.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
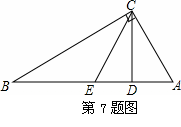
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠B的度数是…………………………………( )
A.60° B.45° C.30° D.75°
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开 始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”,如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1力第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2015次“移位”后,他到达编号为 的点.
始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”,如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1力第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2015次“移位”后,他到达编号为 的点.

查看答案和解析>>
科目:初中数学 来源: 题型:
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2.
其中正确的有( )

A.①②③ B.②④ C.②⑤ D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
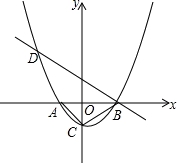
如图,已知抛物线y=m(x+1)(x﹣2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限.
(1)求抛物线的函数表达式.
(2)在第一象限内的抛物线上是否存在点P,使得以A、B、P为顶点的三角形与△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.
(3)若∠DBA=30°,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com