
 如图,抛物线${y_1}={(x-2)^2}+m$与x轴交于点A和B,与y轴交于点C,点D是点C关于抛物线对称轴的对称点,若点A的坐标为(1,0),直线y2=kx+b经过点A,D.
如图,抛物线${y_1}={(x-2)^2}+m$与x轴交于点A和B,与y轴交于点C,点D是点C关于抛物线对称轴的对称点,若点A的坐标为(1,0),直线y2=kx+b经过点A,D.分析 (1)把点A的坐标代入抛物线解析式可求出m的值,进而可得到抛物线的解析式;
(2)首先由抛物线的解析式可求出点C的坐标,再根据函数图象的对称性即可求出点D的坐标;由于点A的坐标已知,进而可求出直线AD的解析式;
(3)结合两个函数图象可知当但直线在抛物线上方时可得到y2>y1的解集.
解答 解:
(1)∵点A(1,0)在抛物线上,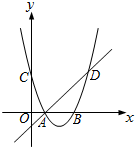
∴(1-2)2+m=0,
∴m=-1,
∴y1=(x-2)2-1;
(2)抛物线y1=(x-2)2-1的对称轴为x=2,与y的交点C的坐标为(0,3),
∵点D是点C关于对称轴x=2的对称点,
∴点D的坐标为(4,3),
直线AD经过点点A,D,
∴$\left\{{\begin{array}{l}{k+b=0}\\{4k+b=3}\end{array}}\right.$,
解得k=1,b=-1,
∴y=x-1;
(3)当1<x<4时,y2>y1.
点评 本题考查二次函数与不等式(组)的知识,同时涉及到用待定系数法求一次函数解析式和二次函数的性质,解题要注意数形结合思想的灵活运用,难度一般.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:解答题
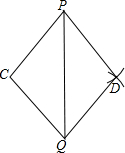 如图,已知△PCQ,按如下步骤作图:①以P为圆心,PC长为半径画弧;②以Q为圆心,QC长为半径画弧,两弧相交于点D;③连接PD、QD.求证:△PCQ≌△PDQ.
如图,已知△PCQ,按如下步骤作图:①以P为圆心,PC长为半径画弧;②以Q为圆心,QC长为半径画弧,两弧相交于点D;③连接PD、QD.求证:△PCQ≌△PDQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,OC为∠AOB内一条直线,下列条件中不能确定OC平分∠AOB的是( )
如图,OC为∠AOB内一条直线,下列条件中不能确定OC平分∠AOB的是( )| A. | ∠AOC=∠BOC | B. | ∠AOB=2∠AOC | C. | ∠AOC+∠COB=∠AOB | D. | $∠BOC=\frac{1}{2}∠AOB$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1022.01(精确到0.01) | B. | 1022(精确到个位) | ||
| C. | 1022.00(精确到0.1) | D. | 1022.010(精确到千分位) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com