
【题目】已知△ABC,AB=AC,BD是∠ABC的角平分线,EF是BD的中垂线,且分别交BC于点E,交AB于点F,交BD于点K,连接DE,DF.
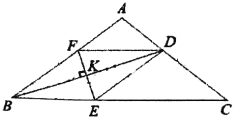
(1)证明:DE//AB;
(2)若CD=3,求四边形BEDF的周长.
【答案】(1)见详解;(2)12
【解析】
(1)由角平分线性质,得到∠ABD=∠CBD,由EF是BD的中垂线,则BE=DE,则∠CBD=∠EDB,则∠ABD=∠EDB,即可得到答案;
(2)先证明四边形BEDF是菱形,由DE∥AB,得到DE=CD=3,即可求出周长;
(1)证明:∵BD是∠ABC的角平分线,
∴∠ABD=∠CBD,
∵EF是BD的中垂线,
∴BE=DE,BF=DF,
∴∠CBD=∠EDB,
∴∠ABD=∠EDB,
∴DE∥AB;
(2)解:与(1)同理,可证DF∥BC,
∴四边形BEDF是平行四边形,
∵BE=DE,
∴四边形BEDF是菱形,
∵AB=BC,DE∥AB,
∴∠C=∠ABC=∠DEC,
∴DE=CD=3,
∴菱形BEDF的周长为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,要在江苏省某林场东西方向的两地之间修一条公路MN,已知C点周围200米范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600米到达B处,测得C在点B的北偏西60°方向上.

(1)MN是否穿过原始森林保护区?为什么?(参考数据:![]() )
)
(2)若修路工程工程需尽快完成.如果由甲、乙两个工程队合做,12天可完成;如果由甲、乙两队单独做,甲队比乙队少用10天完成.求甲、乙两工程队单独完成此项工程所需的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习解直角三角形以后,某兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在水平地面L的影长BC为5米,落在斜坡上的部分影长CD为4米.测得斜CD的坡度i=1:![]() .太阳光线与斜坡的夹角∠ADC=80°,则旗杆AB的高度_____.(精确到0.1米)(参考数据:sin50°=0.8,tan50°=1.2,
.太阳光线与斜坡的夹角∠ADC=80°,则旗杆AB的高度_____.(精确到0.1米)(参考数据:sin50°=0.8,tan50°=1.2,![]() =1.732)
=1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
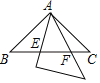
【题目】两个全等的等腰直角三角形,斜边长为2,按如图放置,其中一个三角形45°角的项点与另一个三角形的直角顶点A重合,若三角形ABC固定,当另一个三角形绕点A旋转时,它的角边和斜边所在的直线分别与边BC交于点E、F,设BF=![]() CE=
CE=![]() 则
则![]() 关于
关于![]() 的函数图象大致是( )
的函数图象大致是( )
A.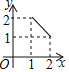 B.
B.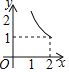 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,重庆欢乐谷的摩天轮是西南地区最高的摩天轮,号称“重庆之限”.摩天轮是一个圆形,直径AB垂直水平地面于点C,最低点B离地面的距离BC为1.6米.某天,妈妈带着洋洋来坐摩天轮,当她站在点D仰着头看见摩天轮的圆心时,仰角为37,为了选择更佳角度为洋洋拍照,妈妈后退了49米到达点D’,当洋洋坐的桥厢F与圆心O在同一水平线时,他俯头看见妈妈的眼睛,此时俯角为42,已知妈妈的眼睛到地面的距离为1.6米,妈妈两次所处的位置与摩天轮在同一平面上,则该摩天轮最高点A离地面的距离AC约是( )
(参考数据:sin37≈0.60,tan37≈0.75,sin42≈0.67,tan42≈0.90)
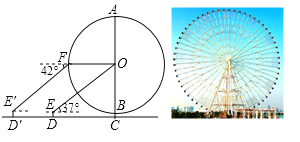
A.118.8米B.127.6米C.134.4米D.140.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
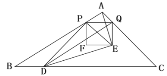
【题目】如图,点E为□ABCD中一点,EA=ED,∠AED=90,点F,G分别为AB,BC上的点,连接DF,AG,AD=AG=DF,且AG⊥DF于点H,连接EG,DG,延长AB,DG相交于点P.
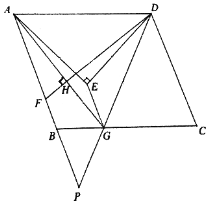
(1)若AH=6,FH=2,求AE的长;
(2)求证:∠P=45;
(3)若DG=2PG,求证:∠AGE=∠EDG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款新产品,通过市场调研后,按三种颜色受欢迎的程度分别对A颜色、B颜色、C颜色的产品在成本的基础上分别加价40%,50%,60%出售(三种颜色产品的成本一样),经过一个季度的经营后,发现C颜色产品的销量占总销量的40%,三种颜色产品的总利润率为51.5%,第二个季度,公司决定对A产品进行升级,升级后A产品的成本提高了25%,其销量提高了60%,利润率为原来的两倍;B产品的销量提高到与升级后的A产品的销量一样,C产品的销量比第一季度提高了50%,则第二个季度的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
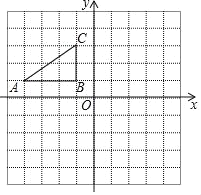
【题目】如图,在平面直角坐标系中,小正方形格子的边长为1,Rt△ABC三个顶点都在格点上,请解答下列问题:
(1)写出A,C两点的坐标;
(2)画出△ABC关于原点O的中心对称图形△A1B1C1;
(3)画出△ABC绕原点O顺时针旋转90°后得到的△A2B2C2,并直接写出点C旋转至C2经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,过
运动,过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,以
,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,同时以
,同时以![]() 为边向下作正方形
为边向下作正方形![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒
秒![]() .
.
(1)点![]() 到直线
到直线![]() 的距离______________;(用含
的距离______________;(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 落在落在
落在落在![]() 上时,求
上时,求![]() 的值;
的值;
(3)设平行四边形![]() 与正方形
与正方形![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最大值.
的最大值.
(4)设![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com