
【题目】计算:
(1)![]()
(2)﹣ ![]()
(3)![]() ﹣4
﹣4
(4)![]() +(1﹣
+(1﹣ ![]() )0 .
)0 .
(5)(2 ![]() +
+ ![]() )(2
)(2 ![]() ﹣
﹣ ![]() )
)
(6)![]() ÷
÷ ![]() +
+ ![]() ×
× ![]() ﹣
﹣ ![]() .
.
【答案】
(1)解:原式= ![]() =
= ![]()
(2)解:原式=﹣ ![]()
(3)解:原式= ![]() ﹣4
﹣4
=10 ![]() ﹣4
﹣4
(4)解:原式= ![]() +1
+1
=5+1
=6
(5)解:原式=12﹣6
=6
(6)解:原式= ![]() +
+ ![]() ﹣2
﹣2 ![]()
=4+ ![]() ﹣2
﹣2 ![]()
=4+ ![]()
【解析】(1)、(2)利用二次根式的性质化简;(3)先把各二次根式化简为最简二次根式,然后约分即可;(4)先把各二次根式化简为最简二次根式,然后利用二次根式的除法法则和零指数幂的意义计算;(5)利用平方差公式计算;(6)先根据二次根式的乘除法则运算,然后化简后合并即可.
【考点精析】掌握零指数幂法则和整数指数幂的运算性质是解答本题的根本,需要知道零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】设ω是一个平面图形,如果用直尺和圆规经过有限步作图(简称尺规作图),画出一个正方形与ω的面积相等(简称等积),那么这样的等积转化称为ω的“化方”.
(1)阅读填空
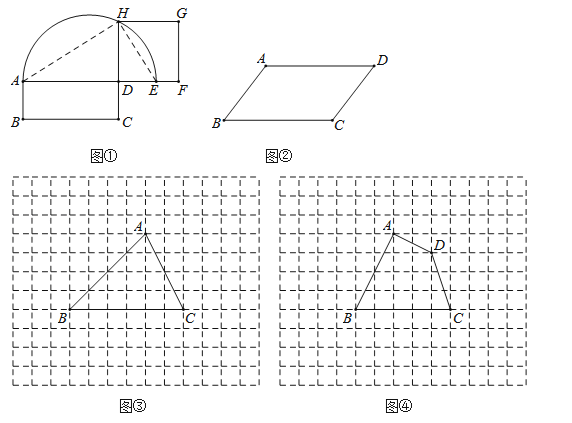
如图①,已知矩形ABCD,延长AD到E,使DE=DC,以AE为直径作半圆.延长CD交半圆于点H,以DH为边作正方形DFGH,则正方形DFGH与矩形ABCD等积.
理由:连接AH,EH.
∵AE为直径,∴∠AHE=90°,∴∠HAE+∠HEA=90°.
∵DH⊥AE,∴∠ADH=∠EDH=90°
∴∠HAD+∠AHD=90°
∴∠AHD=∠HED,∴△ADH∽ .
∴![]() ,即DH2=AD×DE.
,即DH2=AD×DE.
又∵DE=DC
∴DH2= ,即正方形DFGH与矩形ABCD等积.
(2)操作实践
平行四边形的“化方”思路是,先把平行四边形转化为等积的矩形,再把矩形转化为等积的正方形.
如图②,请用尺规作图作出与ABCD等积的矩形(不要求写具体作法,保留作图痕迹).
(3)解决问题三角形的“化方”思路是:先把三角形转化为等积的 (填写图形名称),再转化为等积的正方形.
如图③,△ABC的顶点在正方形网格的格点上,请作出与△ABC等积的正方形的一条边(不要求写具体作法,保留作图痕迹,不通过计算△ABC面积作图).
(4)拓展探究
n边形(n>3)的“化方”思路之一是:把n边形转化为等积的n﹣1边形,…,直至转化为等积的三角形,从而可以化方.
如图④,四边形ABCD的顶点在正方形网格的格点上,请作出与四边形ABCD等积的三角形(不要求写具体作法,保留作图痕迹,不通过计算四边形ABCD面积作图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为「P」,即「P」=![]() +
+![]() .(其中的“+”是四则运算中的加法)
.(其中的“+”是四则运算中的加法)
(1)求点A(﹣1,3),B(![]() ,
,![]() )的勾股值「A」、「B」;
)的勾股值「A」、「B」;
(2)点M在反比例函数![]() 的图象上,且「M」=4,求点M的坐标;
的图象上,且「M」=4,求点M的坐标;
(3)求满足条件「N」=3的所有点N围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列选项中,不能判定两直线平行的是( )
A. 内错角相等,两直线平行
B. 同位角相等,两直线平行
C. 同旁内角相等,两直线平行
D. 同一平面内,垂直于同一条直线的两条直线平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com