
����Ŀ�������һ��ƽ��ͼ�Σ������ֱ�ߺ�Բ�澭��������ͼ����Ƴ߹���ͼ��������һ����������ص������ȣ���ƵȻ�������ô�����ĵȻ�ת����Ϊ�صġ���������
��1���Ķ����
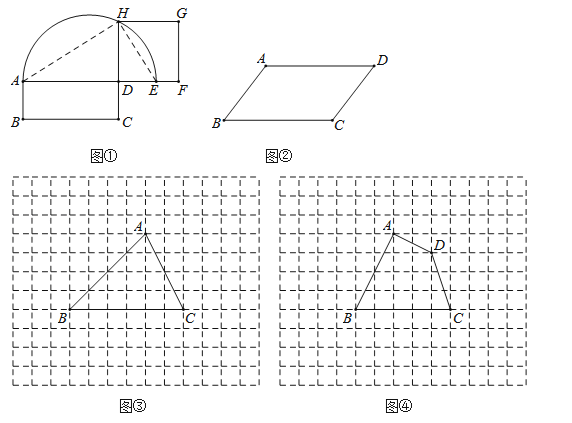
��ͼ�٣���֪����ABCD���ӳ�AD��E��ʹDE=DC����AEΪֱ������Բ���ӳ�CD����Բ�ڵ�H����DHΪ����������DFGH����������DFGH�����ABCD�Ȼ���
���ɣ�����AH��EH��
��AEΪֱ�������AHE=90�㣬���HAE+��HEA=90�㣮
��DH��AE�����ADH=��EDH=90��
���HAD+��AHD=90��
���AHD=��HED�����ADH�� ��
��![]() ����DH2=AD��DE��
����DH2=AD��DE��
�֡�DE=DC
��DH2= ����������DFGH�����ABCD�Ȼ���
��2������ʵ��
ƽ���ı��εġ�������˼·�ǣ��Ȱ�ƽ���ı���ת��Ϊ�Ȼ��ľ��Σ��ٰѾ���ת��Ϊ�Ȼ��������Σ�
��ͼ�ڣ����ó߹���ͼ������ABCD�Ȼ��ľ��Σ���Ҫ��д����������������ͼ�ۼ�����
��3��������������εġ�������˼·�ǣ��Ȱ�������ת��Ϊ�Ȼ��� ����дͼ�����ƣ�����ת��Ϊ�Ȼ��������Σ�
��ͼ�ۣ���ABC�Ķ���������������ĸ���ϣ����������ABC�Ȼ��������ε�һ���ߣ���Ҫ��д����������������ͼ�ۼ�����ͨ�������ABC�����ͼ����
��4����չ̽��
n���Σ�n��3���ġ�������˼·֮һ�ǣ���n����ת��Ϊ�Ȼ���n��1���Σ�����ֱ��ת��Ϊ�Ȼ��������Σ��Ӷ����Ի�����
��ͼ�ܣ��ı���ABCD�Ķ���������������ĸ���ϣ����������ı���ABCD�Ȼ��������Σ���Ҫ��д����������������ͼ�ۼ�����ͨ�������ı���ABCD�����ͼ����
���𰸡���1����HDE��AD��DC����2����ͼ�������������3����������ͼ�������������4����ͼ�����������
��������
�����������1���������������ε��ж�������������ADH�ס�HDE�����ݵ����������ɵ�DH2=AD��DC��
��2���Ȱ�ƽ���ı���ABCDת��Ϊ�Ȼ��ľ���ADMN��Ȼ������������DFGH�����ABMN�Ȼ�������������DFGH��ƽ���ı���ABCD�Ȼ���
��3�����������εĵ�Ϊ���εij����������εĸߵ�һ��Ϊ���εĿ�������ABCת��Ϊ�Ȼ��ľ���MBCD��Ȼ���ӳ�MD��E��ʹDE=DC����MEΪֱ������Բ���ӳ�CD����Բ�ڵ�H����DH��Ϊ����ABC�Ȼ��������ε�һ���ߣ�
��4���ȸ�����AG��EH���õ�AG=2EH������CF=2DF���õ�CFEH=DFAG���ɴ˵ó�S��CEF=S��ADF��S��CDI=S��AEI������S��BCE=S�ı���ABCD������BCE���ı���ABCD�Ȼ���
�����������1����ͼ�٣�����AH��EH����AEΪֱ�������AHE=90�㣬���HAE+��HEA=90������DH��AE�����ADH=��EDH=90�㣬���HAD+��AHD=90�㣬���AHD=��HED�����ADH�ס�HDE����![]() ����DH2=AD��DE������DE=DC����DH2=AD��DC����������DFGH�����ABCD�Ȼ���
����DH2=AD��DE������DE=DC����DH2=AD��DC����������DFGH�����ABCD�Ȼ���
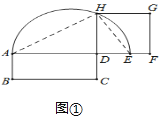
�ʴ�Ϊ����HDE��AD��DC��
��2����ͼ�ڣ��ӳ�AD��E��ʹDE=DM������AH��EH��������ADMN�ij��Ϳ��ֱ����ƽ���ı���ABCD�ĵߣ�������ADMN���������ƽ���ı���ABCD���������AEΪֱ�������AHE=90�㣬���HAE+��HEA=90������DH��AE�����ADH=��EDH=90�㣬���HAD+��AHD=90�㣬���AHD=��HED�����ADH�ס�HDE����![]() ����DH2=AD��DE������DE=DM����DH2=AD��DM����������DFGH�����ABMN�Ȼ�����������DFGH��ƽ���ı���ABCD�Ȼ���
����DH2=AD��DE������DE=DM����DH2=AD��DM����������DFGH�����ABMN�Ȼ�����������DFGH��ƽ���ı���ABCD�Ȼ���

��3����ͼ�ۣ��ӳ�MD��E��ʹDE=DC������MH��EH��������MDBC�ij�������ABC�ĵף�����MDBC�Ŀ�������ABC�ĸߵ�һ�룬������MDBC�����������ABC���������MEΪֱ�������MHE=90�㣬���HME+��HEM=90������DH��ME�����MDH=��EDH=90�㣬���HMD+��MHD=90�㣬���MHD=��HED�����MDH�ס�HDE����![]() ����DH2=MD��DE������DE=DC����DH2=MD��DC����DH��Ϊ����ABC�Ȼ��������ε�һ������
����DH2=MD��DE������DE=DC����DH2=MD��DC����DH��Ϊ����ABC�Ȼ��������ε�һ������
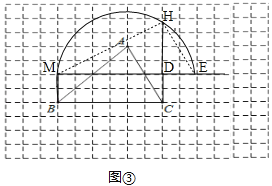
��4����ͼ�ܣ��ӳ�BA��CD���ڵ�F����AG��CF�ڵ�G��EH��CF�ڵ�H����BCE���ı���ABCD�Ȼ����������£���AG��EH����![]() ����AG=2EH������CF=2DF����CFEH=DFAG����S��CEF=S��ADF����S��CDI=S��AEI����S��BCE=S�ı���ABCD������BCE���ı���ABCD�Ȼ���
����AG=2EH������CF=2DF����CFEH=DFAG����S��CEF=S��ADF����S��CDI=S��AEI����S��BCE=S�ı���ABCD������BCE���ı���ABCD�Ȼ���
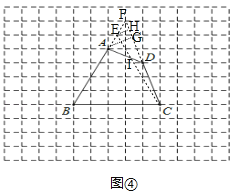


 ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ʾ����AOB����BOC=3��2��ODƽ�֡�BOC��OEƽ�֡�AOC���ҡ�DOE=36�㣬���BOE�Ķ�����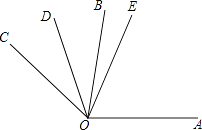
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���BAC=100�㣬DF��EG�ֱ���AB��AC�Ĵ�ֱƽ���ߣ����DAE���ڣ� ��
A.50��
B.45��
C.30��
D.20��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ���������λѡ�ָ�10�������ƽ���ɼ�����9.2�������мijɼ��ķ���Ϊ0.015�� �ҵijɼ��ķ���Ϊ0.035�����ijɼ��ķ���Ϊ0.025�����ijɼ��ķ���Ϊ0.027���ɴ˿�֪
��A���ijɼ����ȶ� ��B���ҵijɼ����ȶ�
��C�����ijɼ����ȶ� ��D�����ijɼ����ȶ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijһ�ܵ�ÿһ����������ͳ�����±���
������£��棩 | 25 | 26 | 27 | 28 |
���� | 1 | 1 | 2 | 3 |
���������ݵ���λ���� �� ������ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԪ���η���x2��4x+2��0����Ϊx1��x2����x1x2����������
A.��4B.4C.��2D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��![]()
��2���� ![]()
��3��![]() ��4
��4
��4��![]() +��1��
+��1�� ![]() ��0 ��
��0 ��
��5����2 ![]() +
+ ![]() ����2
����2 ![]() ��
�� ![]() ��
��
��6��![]() ��
�� ![]() +
+ ![]() ��
�� ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���AOBΪ����ֱ�������Σ�A��4��4�� 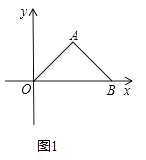
��1����B�����ꣻ
��2����ͼ2����CΪx����������һ���㣬��ACΪֱ�DZ�������ֱ�ǡ�ACD����ACD=90����OD�����AOD�Ķ����� 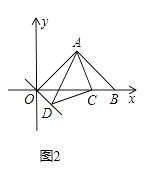
��3����ͼ3������A��y��Ĵ��߽�y����E��FΪx�Ḻ������һ�㣬G��EF���ӳ����ϣ���EGΪֱ�DZ�������Rt��EGH����A��x�ᴹ�߽�EH�ڵ�M����FM����ʽAM=FM+OF�Ƿ����������������֤��������������˵�����ɣ� 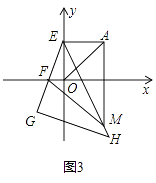
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com