
【题目】已知一元二次方程x2﹣4x+2=0两根为x1、x2,则x1x2=( )
A.﹣4B.4C.﹣2D.2
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s).
(1)当动点P、Q同时运动2s时,则BP=cm,BQ=cm.
(2)当动点P、Q同时运动t(s)时,分别用含有t的式子表示;BP=cm,BQ=cm.
(3)当t为何值时,△PBQ是直角三角形? 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设ω是一个平面图形,如果用直尺和圆规经过有限步作图(简称尺规作图),画出一个正方形与ω的面积相等(简称等积),那么这样的等积转化称为ω的“化方”.
(1)阅读填空
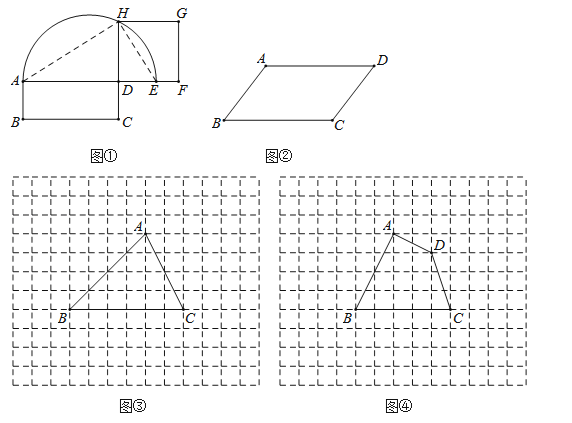
如图①,已知矩形ABCD,延长AD到E,使DE=DC,以AE为直径作半圆.延长CD交半圆于点H,以DH为边作正方形DFGH,则正方形DFGH与矩形ABCD等积.
理由:连接AH,EH.
∵AE为直径,∴∠AHE=90°,∴∠HAE+∠HEA=90°.
∵DH⊥AE,∴∠ADH=∠EDH=90°
∴∠HAD+∠AHD=90°
∴∠AHD=∠HED,∴△ADH∽ .
∴![]() ,即DH2=AD×DE.
,即DH2=AD×DE.
又∵DE=DC
∴DH2= ,即正方形DFGH与矩形ABCD等积.
(2)操作实践
平行四边形的“化方”思路是,先把平行四边形转化为等积的矩形,再把矩形转化为等积的正方形.
如图②,请用尺规作图作出与ABCD等积的矩形(不要求写具体作法,保留作图痕迹).
(3)解决问题三角形的“化方”思路是:先把三角形转化为等积的 (填写图形名称),再转化为等积的正方形.
如图③,△ABC的顶点在正方形网格的格点上,请作出与△ABC等积的正方形的一条边(不要求写具体作法,保留作图痕迹,不通过计算△ABC面积作图).
(4)拓展探究
n边形(n>3)的“化方”思路之一是:把n边形转化为等积的n﹣1边形,…,直至转化为等积的三角形,从而可以化方.
如图④,四边形ABCD的顶点在正方形网格的格点上,请作出与四边形ABCD等积的三角形(不要求写具体作法,保留作图痕迹,不通过计算四边形ABCD面积作图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内有三条直线,如果要使其中两条且只有两条直线平行,那么它们( )
A. 没有交点 B. 只有一个交点
C. 有两个交点 D. 有三个交点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com