
【题目】已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s).
(1)当动点P、Q同时运动2s时,则BP=cm,BQ=cm.
(2)当动点P、Q同时运动t(s)时,分别用含有t的式子表示;BP=cm,BQ=cm.
(3)当t为何值时,△PBQ是直角三角形? 
【答案】
(1)1;2
(2)(3﹣t);t
(3)解:根据题意,得AP=t cm,BQ=t cm.
在△ABC中,AB=BC=3 cm,∠B=60°,
∴BP=(3﹣t)cm.
在△PBQ中,BP=(3﹣t)cm.,BQ=tcm,
若△PBQ是直角三角形,
则只有∠BQP=90°或∠BPQ=90°
① 当∠BQP=90°时,BQ= ![]() BP,
BP,
即t= ![]() (3﹣t),解得t=1;
(3﹣t),解得t=1;
②当∠BPQ=90°时,BP= ![]() BQ,
BQ,
即3﹣t= ![]() t.解得t=2.
t.解得t=2.
答:当t=1s或t=2s时,△PBQ是直角三角形

【解析】解:(1)BQ=1×2=2(cm),BP=3﹣2=1(cm), 所以答案是1,2;(2)BP=(3﹣t) cm,BQ=tcm,
所以答案是(3﹣t),t;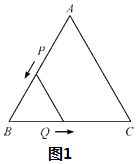
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( ) 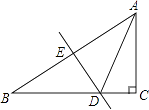
A.6
B.6 ![]()
C.9
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]()
(1)若点P为AB的中点,直接写出点P对应的数;
(2)数轴的原点右侧是否存在点P,使点P到点A、点B的距离之和为8?若存在,请求出x的值;若不存在,说明理由;
(3)现在点A、点B分别以每秒2个单位长度和每秒0.5个单位长度的速度同时向右运动,同时点P以每秒6个单位长度的速度从表示数1的点向左运动.当点A与点B之间的距离为3个单位长度时,求点P所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到AC的距离为3,则点P到AB的距离为( ) 
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年约5000名初三学生参加数学中考,从中抽取300名考生的数学成绩进行分析,则在该调查中,样本指的是 ( )
A. 300 B. 300名 C. 5000名考生的数学成绩 D. 300名考生的数学成绩
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com