
【题目】如图1,在平面直角坐标系中,△AOB为等腰直角三角形,A(4,4) 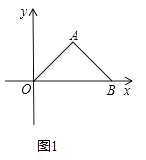
(1)求B点坐标;
(2)如图2,若C为x轴正半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°连OD,求∠AOD的度数; 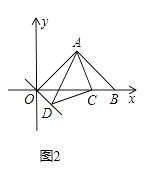
(3)如图3,过点A作y轴的垂线交y轴于E,F为x轴负半轴上一点,G在EF的延长线上,以EG为直角边作等腰Rt△EGH,过A作x轴垂线交EH于点M,连FM,等式AM=FM+OF是否成立?若成立,请证明:若不成立,说明理由. 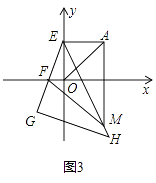
【答案】
(1)解:如图所示,作AE⊥OB于E,

∵A(4,4),
∴OE=4,
∵△AOB为等腰直角三角形,且AE⊥OB,
∴OE=EB=4,
∴OB=8,
∴B(8,0)
(2)解:方法一:如图所示,作AE⊥OB于E,DF⊥OB于F,
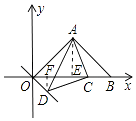
∵△ACD为等腰直角三角形,
∴AC=DC,∠ACD=90°
即∠ACF+∠DCF=90°,
∵∠FDC+∠DCF=90°,
∴∠ACF=∠FDC,
又∵∠DFC=∠AEC=90°,
∴△DFC≌△CEA(AAS),
∴EC=DF,FC=AE,
∵A(4,4),
∴AE=OE=4,
∴FC=OE,即OF+EF=CE+EF,
∴OF=CE,
∴OF=DF,
∴∠DOF=45°,
∵△AOB为等腰直角三角形,
∴∠AOB=45°,
∴∠AOD=∠AOB+∠DOF=90°;
方法二:如图所示,过C作CK⊥x轴交OA的延长线于K,
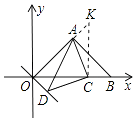
则△OCK为等腰直角三角形,OC=CK,∠K=45°,
又∵△ACD为等腰Rt△,
∴∠ACK=90°﹣∠OCA=∠DCO,AC=DC,
∴△ACK≌△DCO(SAS),
∴∠DOC=∠K=45°,
∴∠AOD=∠AOB+∠DOC=90°
(3)解:AM=FM+OF成立,理由:
方法一:如图所示,在AM上截取AN=OF,连EN.

∵A(4,4),
∴AE=OE=4,
又∵∠EAN=∠EOF=90°,AN=OF,
∴△EAN≌△EOF(SAS),
∴∠OEF=∠AEN,EF=EN,
又∵△EGH为等腰直角三角形,
∴∠GEH=45°,即∠OEF+∠OEM=45°,
∴∠AEN+∠OEM=45°
又∵∠AEO=90°,
∴∠NEM=45°=∠FEM,
又∵EM=EM,
∴△NEM≌△FEM(SAS),
∴MN=MF,
∴AM﹣MF=AM﹣MN=AN,
∴AM﹣MF=OF,
即AM=FM+OF;
方法二:如图所示,在x轴的负半轴上截取ON=AM,连EN,MN,
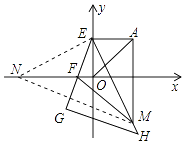
则△EAM≌△EON(SAS),
∴EN=EM,∠NEO=∠MEA,
即∠NEF+∠FEO=∠MEA,
而∠MEA+∠MEO=90°,
∴∠NEF+∠FEO+∠MEO=90°,
而∠FEO+∠MEO=45°,
∴∠NEF=45°=∠MEF,
∴△NEF≌△MEF(SAS),
∴NF=MF,
∴AM=OF=OF+NF=OF+MF,
即AM=FM+OF.
【解析】(1)因为△AOB为等腰直角三角形,A(4,4),作AE⊥OB于E,则B点坐标可求;(2)作AE⊥OB于E,DF⊥OB于F,求证△DFC≌△CEA,再根据等量变换,即可求出∠AOD的度数可求;(3)在AM上截取AN=OF,连EN,易证△EAN≌△EOF,再根据角与角之间的关系,证明△NEM≌△FEM,则有AM﹣MF=OF,即可求证等式成立.
【考点精析】通过灵活运用等腰直角三角形,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】设ω是一个平面图形,如果用直尺和圆规经过有限步作图(简称尺规作图),画出一个正方形与ω的面积相等(简称等积),那么这样的等积转化称为ω的“化方”.
(1)阅读填空
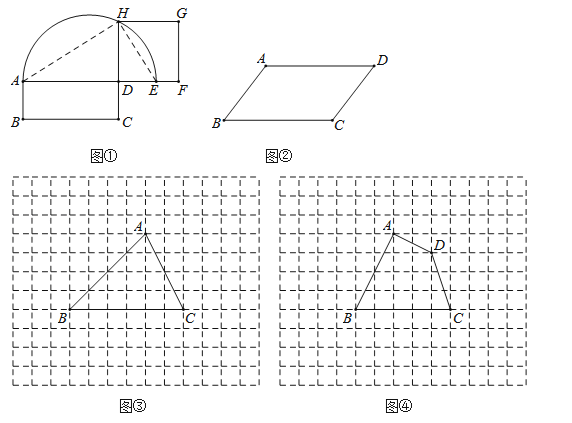
如图①,已知矩形ABCD,延长AD到E,使DE=DC,以AE为直径作半圆.延长CD交半圆于点H,以DH为边作正方形DFGH,则正方形DFGH与矩形ABCD等积.
理由:连接AH,EH.
∵AE为直径,∴∠AHE=90°,∴∠HAE+∠HEA=90°.
∵DH⊥AE,∴∠ADH=∠EDH=90°
∴∠HAD+∠AHD=90°
∴∠AHD=∠HED,∴△ADH∽ .
∴![]() ,即DH2=AD×DE.
,即DH2=AD×DE.
又∵DE=DC
∴DH2= ,即正方形DFGH与矩形ABCD等积.
(2)操作实践
平行四边形的“化方”思路是,先把平行四边形转化为等积的矩形,再把矩形转化为等积的正方形.
如图②,请用尺规作图作出与ABCD等积的矩形(不要求写具体作法,保留作图痕迹).
(3)解决问题三角形的“化方”思路是:先把三角形转化为等积的 (填写图形名称),再转化为等积的正方形.
如图③,△ABC的顶点在正方形网格的格点上,请作出与△ABC等积的正方形的一条边(不要求写具体作法,保留作图痕迹,不通过计算△ABC面积作图).
(4)拓展探究
n边形(n>3)的“化方”思路之一是:把n边形转化为等积的n﹣1边形,…,直至转化为等积的三角形,从而可以化方.
如图④,四边形ABCD的顶点在正方形网格的格点上,请作出与四边形ABCD等积的三角形(不要求写具体作法,保留作图痕迹,不通过计算四边形ABCD面积作图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.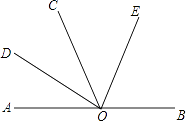
(1)填空:与∠AOE互补的角是;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我市参加中考的人数大约有41300人,将41300用科学记数法表示为( )
A.413×102
B.41.3×103
C.4.13×104
D.0.413×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内有三条直线,如果要使其中两条且只有两条直线平行,那么它们( )
A. 没有交点 B. 只有一个交点
C. 有两个交点 D. 有三个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列选项中,不能判定两直线平行的是( )
A. 内错角相等,两直线平行
B. 同位角相等,两直线平行
C. 同旁内角相等,两直线平行
D. 同一平面内,垂直于同一条直线的两条直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 延长线段AB和延长线段BA的含义相同
B. 射线AB和射线BA是同一条射线
C. 经过两点可以画一条直线,并且只能画一条直线
D. 延长直线AB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com