
【题目】如图,在等边![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,
上,![]() ,线段
,线段![]() 交于点
交于点![]()
![]() 求证:
求证:![]()
![]() 连接
连接![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
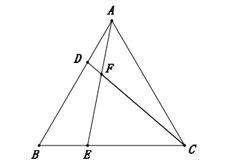
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)证明△ABE△CAD即可;
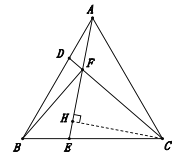
(2)过点C作CH⊥AE,垂足为H,通过证明△BFC△CHA,得到CF=AH,再证明∠FCH=30°,由30°角所对直角边等于斜边的一半,得到CF=2FH,进而可以得到AF=FH,即可得到结论.
(1)∵△ABC等边三角形ABC中,∴∠B=∠BCA=∠CAB=60°,AB=CA=BC.
在△ABE和△CAD中,∵BE=AD,∠B=∠CAB,AB=CA,∴△ABE△CAD,∴AE=CD;
(2)过点C作CH⊥AE,垂足为H,∴∠CHA=90°,∴∠BFC=90°,∠BFC=∠CHA.
∵△ABE△CAD,∴∠BAE=∠ACD.
∵∠CAB-∠BAE=∠BCA-∠ACD,即∠CAE=∠BCD.
在△BFC和△CHA中,∵∠BFC=∠CHA,∠BCD=∠CAE,BC=CA,∴△BFC△CHA,∴CF=AH.
∵∠CFE=∠CAE+∠ACD =∠CAE+∠BAE=∠CAB=60°.
∴∠FCH=180°-∠CHA-∠CFE =180°-90°-60°=30°,∴CF=2FH,∴AH=2FH,即AF+FH=2FH,∴AF=FH,∴CF=2AF.


科目:初中数学 来源: 题型:
【题目】玲玲和牛牛相约在小区笔直的步行道上健步走锻炼身体.两人都从步行道起点![]() 向终点
向终点![]() 走去.牛牛出发
走去.牛牛出发![]() 分钟后,玲玲出发.又过了
分钟后,玲玲出发.又过了![]() 分钟,牛牛停下来接了
分钟,牛牛停下来接了![]() 分钟的电话,玲玲则以原速继续步行,与牛牛相遇后,玲玲的速度减少到原来的
分钟的电话,玲玲则以原速继续步行,与牛牛相遇后,玲玲的速度减少到原来的![]() 走向终点
走向终点![]() .牛牛接完电话后,提高速度向终点
.牛牛接完电话后,提高速度向终点![]() 走去,
走去,![]() 分钟后刚好追上玲玲,到达终点
分钟后刚好追上玲玲,到达终点![]() 后立即调头以提速后的速度返回起点
后立即调头以提速后的速度返回起点![]() (调头时间忽略不计),玲玲、牛牛两人相距的路程
(调头时间忽略不计),玲玲、牛牛两人相距的路程![]() (米)与牛牛出发的时间
(米)与牛牛出发的时间![]() (分钟)之间的关系如图所示.
(分钟)之间的关系如图所示.

(1)牛牛开始健步走的速度为_______米/分;
(2)求玲玲开始健步走的速度和牛牛提速后的速度;
(3)玲玲走到终点![]() 后,停下来休息了一会儿.牛牛回到起点
后,停下来休息了一会儿.牛牛回到起点![]() 后,立即调头仍以提速后的速度走向终点
后,立即调头仍以提速后的速度走向终点![]() ,玲玲休息
,玲玲休息![]() 分钟后以减速后的速度调头走向起点
分钟后以减速后的速度调头走向起点![]() 两人恰好在
两人恰好在![]() 中点处相遇,求步行道
中点处相遇,求步行道![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,点E在AD边上,DE>AE,连接BE,将△ABE沿着BE翻折得到△BFE,射线EF交BC于G,若点G为BC的中点,FG=1,DE=6,则AE的长 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:
(1)求出足球和篮球的单价;
(2)若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?
(3)在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
关于x的方程:![]() 的解是
的解是![]() ,
,![]() ;
;![]() 即
即![]() 的解是
的解是![]() ;
;![]() 的解是
的解是![]() ,
,![]() ;
;![]() 的解是
的解是![]() ,
,![]() ;
;![]()
![]() 请观察上述方程与解的特征,比较关于x的方程
请观察上述方程与解的特征,比较关于x的方程![]() 与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
![]() 由上述的观察、比较、猜想、验证,可以得出结论:
由上述的观察、比较、猜想、验证,可以得出结论:
如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角板ABC的斜边AB与量角器的直径重合,点D是量角器上60°刻度线的外端点,连接CD交AB于点E,则∠CEB的度数为( )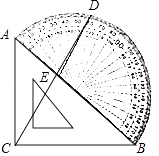
A.60°
B.65°
C.70°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+ ![]() 经过A(1,0),B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边三角形ABC.
经过A(1,0),B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边三角形ABC.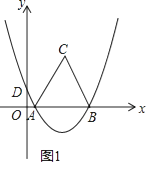
(1)求抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点M,是S△ABM= ![]() S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系及∠APB的度数,并说明理由;
②若AF=BE,当点E由A运动到C时,请直接写出点P经过的路径长.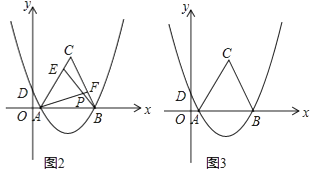
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com