
【题目】数学课上张老师将课本![]() 页第
页第![]() 题进行了改编,图形不变.请你完成下面问题.
题进行了改编,图形不变.请你完成下面问题.
![]() 如图,
如图,![]() .求证:
.求证:![]()
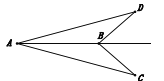
![]() 如图,
如图,![]() .求证:
.求证:![]()
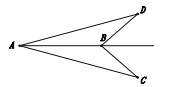
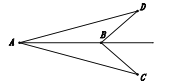
![]() 如图,
如图,![]() 求证:
求证:![]()
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
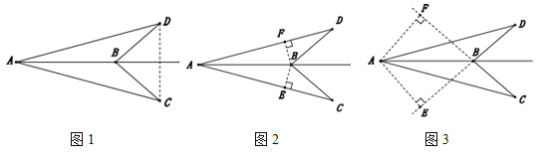
(1)连接CD.根据等边对等角,得到∠BCD=∠BDC,进而得到∠ACD=∠ADC.根据等角对等边得到AC=AD.由SSS即可得到结论;
(2)过点B分别作BE⊥AC,BF⊥AD,垂足分别为E,F.根据角平分线的性质得到BE=BF.再由HL证明Rt△BCERt△BDF,根据全等三角形对应角相等得到∠C=∠D,进而由AAS即可证明△ABC△ABD;
(3)过点A分别作AE⊥BD,AF⊥BC,垂足分别为E,F.先证明点A在∠EBF的平分线上,由角平分线的性质即可得到AE=AF.由HL证明Rt△AED≌Rt△AFC,由全等三角形对应角相等得到∠C=∠D.根据AAS即可证明△ABC≌△ABD.
(1)连接CD.
∵BC=BD,∴∠BCD=∠BDC.
∵∠ACB==∠ADB,∴∠ACB+∠BCD=∠ADB+∠BDC,即∠ACD=∠ADC,∴AC=AD.
在△ABC和△ABD中,∵AC=AD,BC=BD,AB=AB,∴△ABC≌△ABD;
(2)过点B分别作BE⊥AC,BF⊥AD,垂足分别为E,F,∴∠BEC=∠BFD=90°.
∵∠CAB=∠DAB,即点B在∠CAD的平分线上,BE⊥AC,BF⊥AD,垂足分别为E,F,∴BE=BF.
在Rt△BCE和Rt△BDF中,∵BC=BD,BE=BF,∴Rt△BCE≌Rt△BDF,∴∠C=∠D.
在△ABC和△ABD中,∵∠C=∠D,∠CAB=∠DAB,AB=AB,∴△ABC≌△ABD;
(3)如图3,过点A分别作AE⊥BD,AF⊥BC,垂足分别为E,F,∴∠AED=∠AFC=90°.
∵∠ABC+∠ABF=∠ABD+∠ABE=180°,∠ABC=∠ABD,∴∠ABF=∠ABE,即点A在∠EBF的平分线上.
∵AE⊥BD,AF⊥BC,垂足分别为E,F,∴AE=AF.
在Rt△AED和Rt△AFC中,∵AD=AC,AE=AF,∴Rt△AED≌Rt△AFC,∴∠C=∠D.
在△ABC和△ABD中,∵∠C=∠D,∠ABC=∠ABD,AB=AB,∴△ABC≌△ABD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为评估九年级学生的学习成绩状况,以应对即将到来的中考做好教学调整,某中学抽取了部分参加考试的学生的成绩作为样本分析,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
(1)求本中学成绩类别为“中”的人数;
(2)求出扇形图中,“优”所占的百分比,并将条形统计图补充完整;
(3)该校九年级共有1000人参加了这次考试,请估算该校九年级共有多少名学生的数学成绩达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
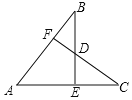
【题目】如图,已知AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE与CF交于点D,则下列结论中不正确的是( )
A. ![]() B.
B. ![]() C. 点D在
C. 点D在![]() 的平分线上D. 点D是CF的中点
的平分线上D. 点D是CF的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】便民服装店的老板在株洲看到一种夏季衬衫,就用8000元购进若干件,以每件58元的价格出售,很快售完,又用17600元购进同种衬衫,数量是第一次的2倍每件进价比第一次多了4元,服装店仍按每件58元出售,全部售完,问该服装店两次一共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF,连接AF,BF,DE,CE,分别交于H,G.求证: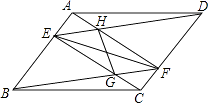
(1)EF与GH互相平分;
(2)在不添加任何辅助线和字母的条件下,请直接写出图中所有的全等的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司员工分别在A、B、C三个住宅区,A区有30人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在( )
![]()
A.A区B.B区C.C区D.A.B两区之间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com