
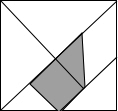
 如图,是被称为“东方魔板”的七巧板,小明随意的向正方形内扎飞镖(线段的粗细忽略不计),则扎飞镖一次恰扎中阴影区域的概率为$\frac{3}{16}$.
如图,是被称为“东方魔板”的七巧板,小明随意的向正方形内扎飞镖(线段的粗细忽略不计),则扎飞镖一次恰扎中阴影区域的概率为$\frac{3}{16}$. 分析 根据一般说的七巧板,两个大三角形分别占大正方形的$\frac{1}{4}$,一个中三角形占正方形的$\frac{1}{8}$,一个正方形占正方形的$\frac{1}{8}$,一个平行四边形都是占正方形的$\frac{1}{8}$,两个小三角形分别占正方形的$\frac{1}{16}$,根据几何概率的定义求概率,即可解答.
解答 解:设正方形的面积为S,
∵一个正方形占正方形的$\frac{1}{8}$,小三角形占正方形的$\frac{1}{16}$,
∴阴影部分的面积为:($\frac{1}{8}+\frac{1}{16}$)S=$\frac{3}{16}$S,
∴则扎飞镖一次恰扎中阴影区域的概率为$\frac{3}{16}$S÷S=$\frac{3}{16}$.
故答案为:$\frac{3}{16}$.
点评 本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ③④⑤ | C. | ④⑤ | D. | ④⑤⑥ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
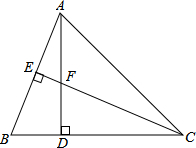 如图,在△ABC中,AD⊥BC于点D,AD=CD=2,过点C作CE⊥AB,交AD于点F,若BD=DF=2$\sqrt{2}$-2,CF=2BE,则AC的长为$2\sqrt{2}$.
如图,在△ABC中,AD⊥BC于点D,AD=CD=2,过点C作CE⊥AB,交AD于点F,若BD=DF=2$\sqrt{2}$-2,CF=2BE,则AC的长为$2\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
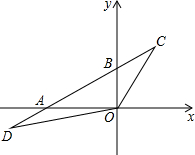 如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过点A(-4,0)、B(0,2)两点,点C、D在直线AB上,C的纵坐标为3,点D在第三象限,且△OBC与△OAD的面积相等,则点D的坐标为(-6,-1).
如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过点A(-4,0)、B(0,2)两点,点C、D在直线AB上,C的纵坐标为3,点D在第三象限,且△OBC与△OAD的面积相等,则点D的坐标为(-6,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
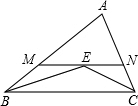 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=15,则线段MN的长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=15,则线段MN的长为( )| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0•a不是单项式 | B. | -$\frac{xyz}{3}$的系数是-$\frac{1}{3}$ | ||
| C. | -$\frac{abc}{4}$的系数是-4 | D. | x3y的系数是0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com